TOPICS

2025年度 第２回の申し込みがスタートしたので、いつものように前回（2025年度 第１回）の検定で正答率が低かった問題を、ふり返ります。
今回は10級の問題です。

【問題】
図１のように、黒いあめ(●)と白いあめ(○)があります。

(1)　あめは全部で何個ありますか。
(2)　図２のような、黒いあめ１個と白いあめ２個が入った袋をつくります。全部で何袋できますか。
(3)　(2)で、白いあめは何個のこりますか。また、のこった白いあめを全部つかって(2)と同じ袋をつくるとき、黒いあめはあと何個あればよいですか。

正答率は、(1)が 72.9％、(2)が76.3％、(3)が44.3％ でした。

(1)は数えるだけの問題ですが、工夫せずに数えると、数え間違えをしやすいです。

どんな工夫ができますか？

以前、数え方を答える問題を出題したことがあり、そのときに子どもたちが実際に行った工夫をまとめていますので、 こちら もご覧ください。

ただ、(2)で「●１個＋○２個」の組み合わせの数を聞いているので、そのことを踏まえて数える方法もありますね。

では、(2)です。

黒あめ１個と白あめ２個を袋に入れるので、●１個と○２個を囲んで、袋がいくつできるか考えます。すると、次の図のように９袋できます。

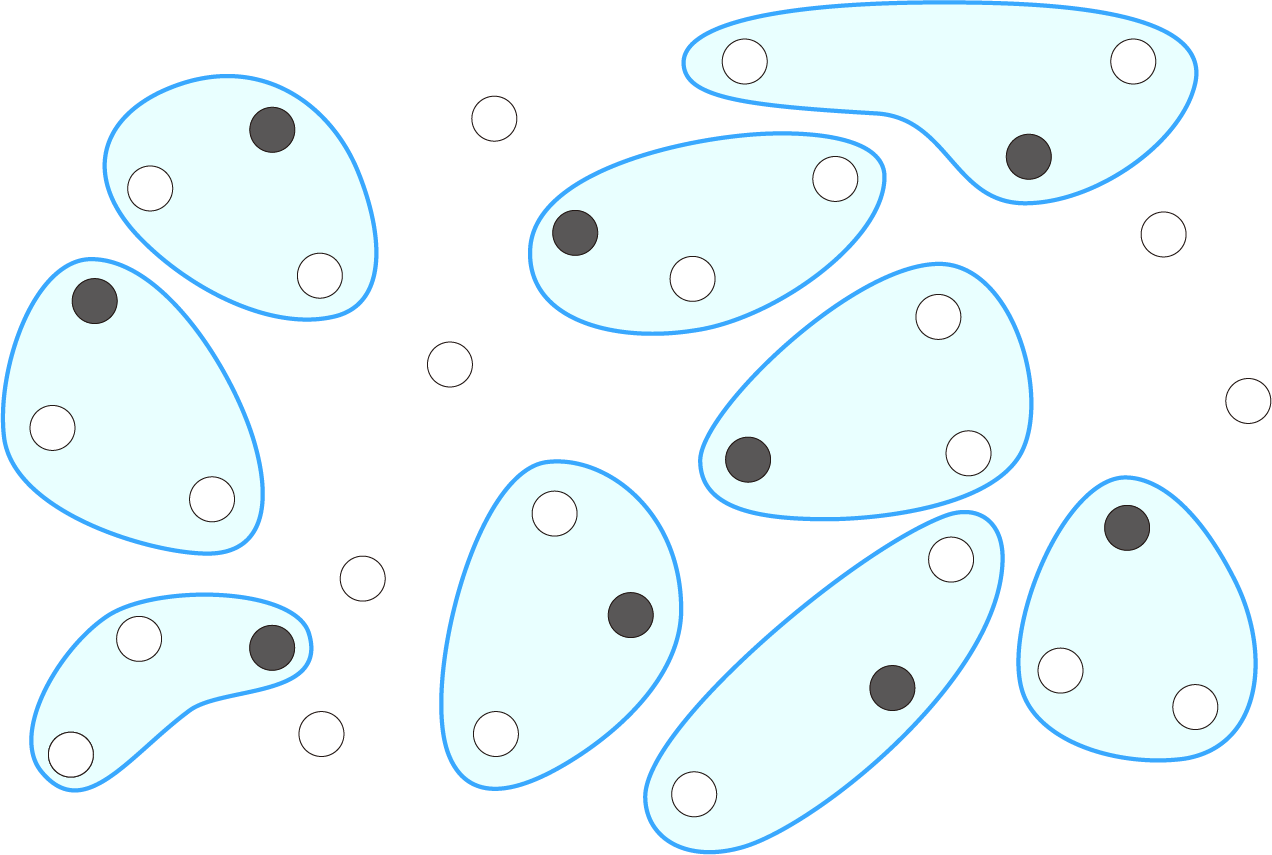
ここで、(1)に戻ってみましょう。１つの袋にあめは３個ずつ入っているので、かけ算を知っている子であれば、袋に入っているあめの数が 3×9＝27(個)と分かります。そして、袋に入っていない○の数は６個なので、全部で 27＋6＝33(個)と分かります。

ちなみに、●と○を分けて数えると、●は９個、○は24個なので、あめは全部で 9＋24＝33(個)です。

さらに、１つの袋には、○が●の２倍の数入るので、9×2＝18(個) から、●９個と○24個では、○のほうが余ることがわかります。また、袋の数と●の数は同じになるので、９袋できると分かります。

10級を受ける子には少々高度な考え方ですが、こんな考え方ができるんだよと気づかせてあげると、思考力が伸びていくでしょう。

ちなみに正答以外の解答類型と反応率は、次の通りです。

８個：6.4％　　10個：2.8％　　３個：2.5％　　11個：2.5％
７個：1.4％　　無回答：2.2％　　その他：5.9％

７個、８個、10個と答えた子は、●を数え間違えて、「●の数＝袋の数」と考えたのかもしれません。
11個と答えた子は、余った○６個を３個ずつ２つの袋に入れて、9＋2＝11（袋）と考えたのかもしれません。

最後に(3)です。

残った白いあめは６個でした。
これを１つの袋に２個ずつ入れるので、○２個の袋が３袋できます。

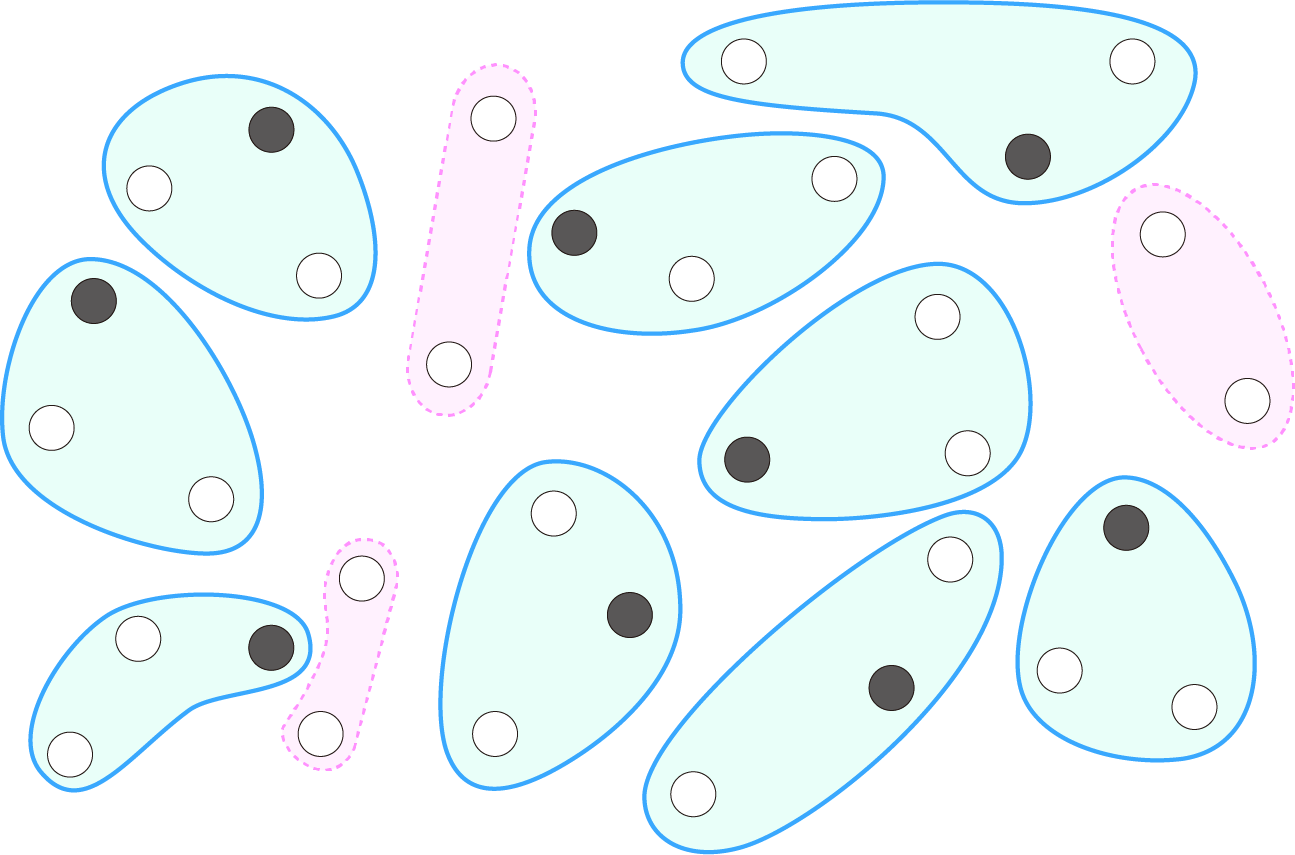
この３袋に●を１個ずつ入れればよいので、●はあと３個あればよいことがわかります。

白いあめ６個と黒いあめ３個の両方ができた子は44.3％でしたが、白いあめのみ正解できた子は13.1％でした。合わせて 44.3＋13.1＝57.4％なのですが、(1)と(2)の正答率から考えると、もう少しできて欲しかったなと思います。

では、誤答の解答類型と反応率を見てみましょう。

【白いあめ】
24個：10.0％　　５個：5.0％　　４個：4.5％　　１個：2.5％
８個：2.2％　　７個：1.7％　　22個：1.7％　　23個：1.7％
０個：1.4％　　２個：1.4％　　９個：1.1％　　無回答：2.2％

24個は、白いあめの数です。「のこりますか」という問いをしっかり読んでいなかったのでしょう。22個、23個も同様ですね。こちらは白いあめの数の数え間違いもしています。
５個、４個、８個、７個、９個は、(2)を間違えた子でしょう。
(2)で８袋と答えた子は、24－(8×2)＝4(個)、10袋と答えた子は、24－(10×2)＝4(個)、７袋と答えた子は、24－(7×2)＝10(個)となります。
しかし、10個という誤答の子はいないので、そもそも24個を数え間違えているのでしょう。

【黒いあめ】
２個：16.4％　　９個：13.1％　　０個：4.2％　　８個：2.8％
10個：2.8％　　４個：2.2％　　６個：1.9％　　７個：1.1％
無回答： 2.2％

また、白いあめの数は間違えているが黒いあめは３個と答えられた子は5.6％で、合わせて44.3＋5.6＝49.6％ です。

９個は、黒いあめの数です。こちらも同様に、問題文をちゃんと理解していない結果です。

では、最も多かった２個はどうでしょうか。
２個と答えていた回答が白を何個と答えていたかの類型と反応率は、次の通りです。

６個：51.8％　　５個：21.4％　　４個：17.9％　　１個：7.1％　　３個：1.8％

６個と答えた子が５割以上いるので、のこった○６個を１袋に３個ずつ分けて２袋＝●２個と考えたのかもしれません。５個と答えた子は２袋つくって○が１個あまると考え、４個と答えた子は当然２袋＝●２個となりますね。

さて、この問題は2016年に出題した問題の類題で、前回は(2)と、(3)の黒いあめ　のみ問いました。
そこで、対応する問題の正答率を比較すると、次のようになります。

(2)：前回60.4％、今回76.3％　　(3)：前回46.6％、今回49.9％

(3)では、残った白いあめを数える段階や、そこから必要な黒あめを求める段階で正答できない子が多く見られました。正答率44.3％に加え、白いあめのみ正解した子を含めても57.4％にとどまり、(1)や(2)の正答率と比べると、思考のステップが増えるほど小さなミスが積み重なりやすいことがわかります。

今回の結果を見ると、(1)の総数を数えるステップは、黒と白を分けて数えるなど少し工夫が必要であるため、正答率は72.9％にとどまりました。一方で(2)は「袋の条件」が明確に与えられているため、段階が単純化され、正答率は76.3％とやや高くなっています。つまり、条件が整理されていて段階的に操作できるほうが、子どもたちは正答しやすい傾向にあると考えられます。

このことから、「条件を整理して段階的に考える力」と「全体の数を正確に把握する力」の両方が重要であることが示されます。家庭学習や授業では、まず全体の数を把握させた上で、条件に沿って袋の数や残りのあめを求めるステップを意識させる練習を取り入れると、誤答を減らし思考力を伸ばすことにつながります。

また、(2)の正答率は前回より15.9ポイント上昇しており、今回(1)を追加して「全体の数を把握させた」影響があった可能性があります。段階的に思考を積み重ねる学習が効果的であることが改めて確認でき、今後の指導でもこのアプローチを意識するとよいでしょう。