問題サンプル
思考力検定では、
次のような問題が出題されます。
(実際の問題には色はついていません)
線でむすぼう
- 内容
- 空間と形
- 思考力
- 筋道を立てて考える力
重なっている順番
- 内容
- 空間と形
- 思考力
- ものの形を認識・想像する力
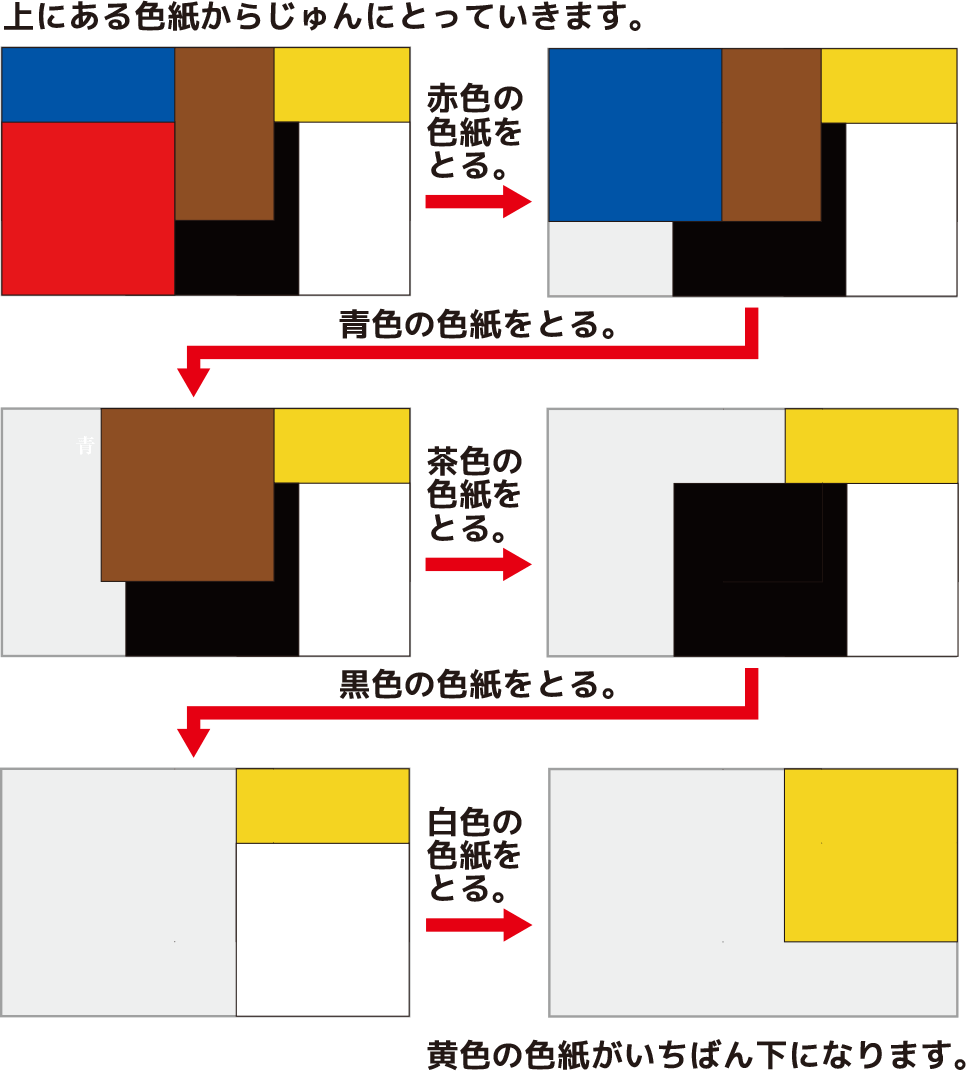
同じ大きさの正方形の色紙6まいを、長方形のはこに重ねて入れたら、図のように、赤色の色紙がいちばん上になりました。赤、白、黄、青、黒、茶の色紙は、どのように重なっていますか。上からじゅんに、色紙の色を書きなさい。

じゃんけん
- 内容
- データと不確実性
- 思考力
- 情報・条件を使い
こなす力
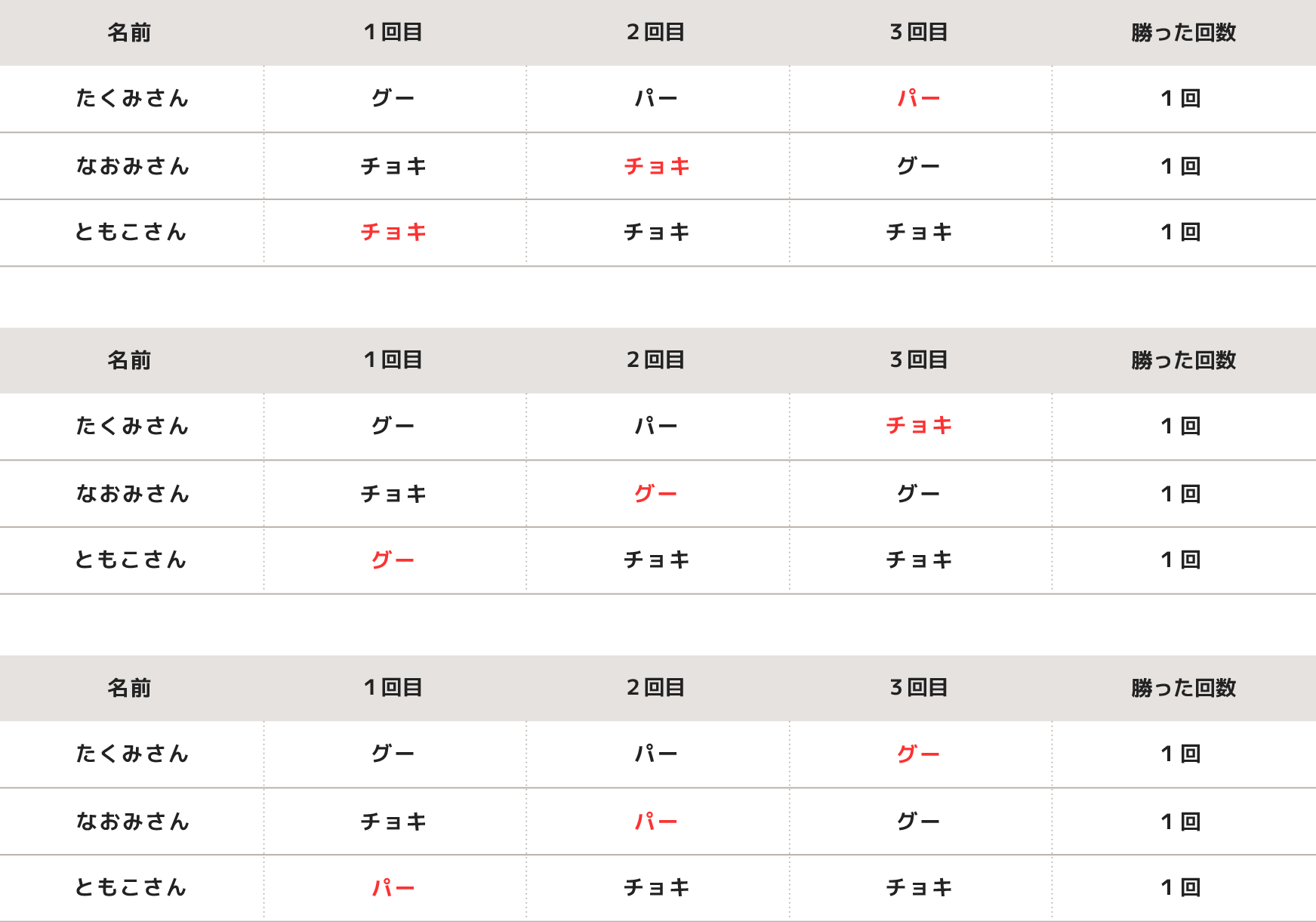
たくみさん、なおみさん、ともこさんの3人がじゃんけんをしました。3回じゃんけんをして、3人とも1回ずつ勝ったそうです。表は、3人がグー、チョキ、パーのどれを出したかをまとめたものです。
表のあいているところに、グー、チョキ、パーのどれかを書き入れなさい。ただし、1回のじゃんけんでは、1人だけ勝つ場合と2人が勝つ場合とあいこになる場合があります。答えが何通りか考えられる場合は、1通りだけ答えなさい。

カレンダー
- 内容
- 変化と関係
- 思考力
- 情報・条件を使いこなす力
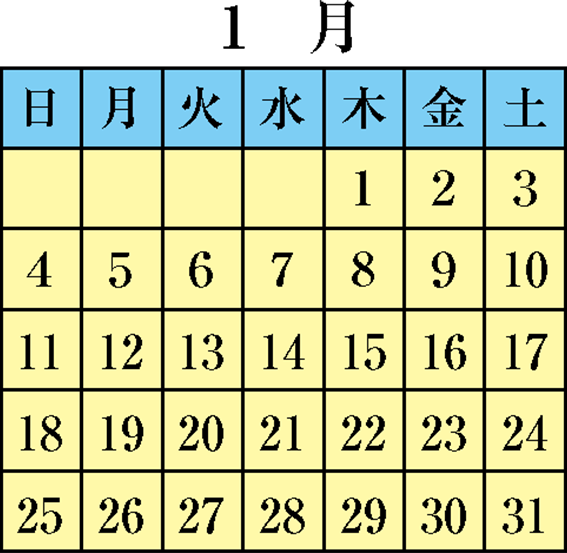
図は、ある年の1月のカレンダーです。この年はうるう年で、2月29日まであります。
- (1) 1月1日は木曜日ですが、次に1日が木曜日になるのは何月ですか。なお、1か月が30日までの月は4月、6月、9月、11月で、31日までの月は1月、3月、5月、7月、8月、10月、12月です。
- (2) この年の5月5日は何曜日ですか。
展開図
- 内容
- 空間と形
- 思考力
- ものの形を認識・想像する力
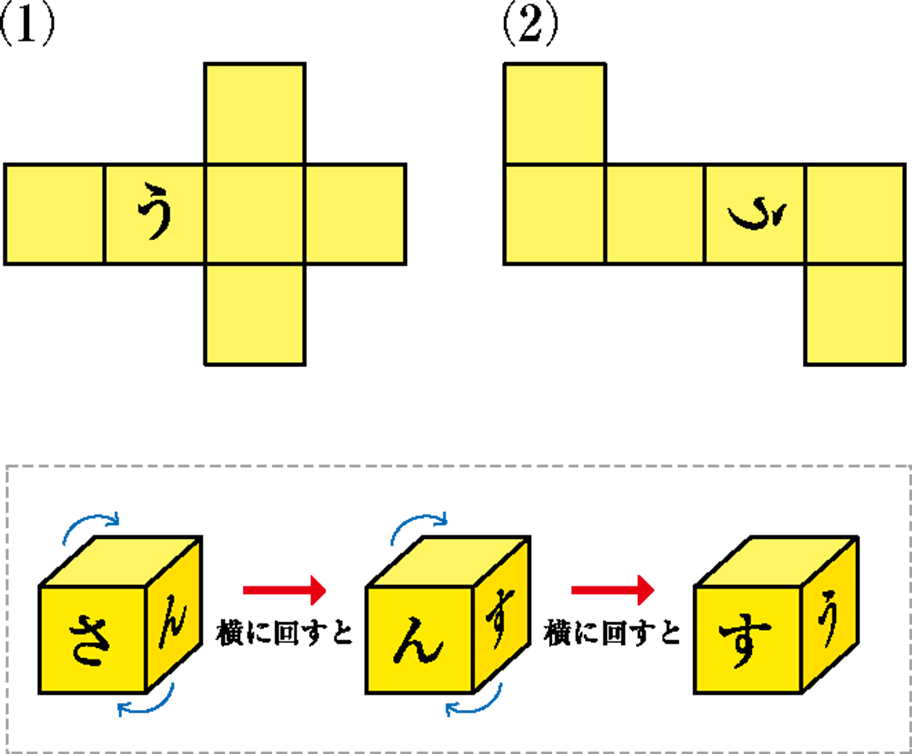
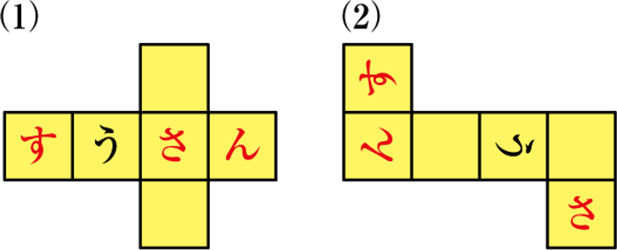
(1)、(2)は立方体の展開図です。この展開図を組み立てて下の図のように横に回したとき、順序正しく「さんすう」と読めるように、残りの文字を図に書き入れなさい。ただし、文字の向きも正しく書き入れること。
◯に数を入れよう
- 内容
- 数と量
- 思考力
- 情報・条件を使いこなす力
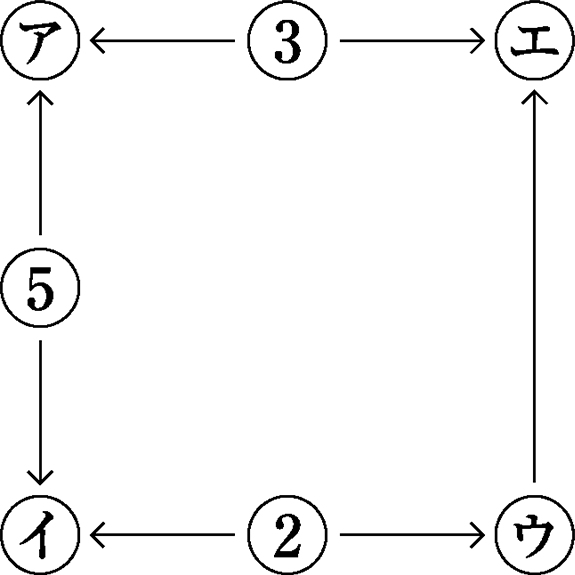
図のように、◯の中に自然数が書かれていて、1つの◯から別の◯に矢印がひかれています。この矢印には(例)のようなきまりがあります。
- (例)18は6でわりきれることを、⑥→⑱と表します。
また、①→⑱、⑦→⑦と表すこともできます。
- (1) アにあてはまる自然数を、小さいものから順に2つ答えなさい。
- (2) イにあてはまる2けたの自然数は何個ありますか。
- (3) エにあてはまる100以下の自然数は、最大で何個あると考えられますか。
デジタル時計
- 内容
- 変化と関係
- 思考力
- 情報・条件を使いこなす力
今、ちょうど午前11時を示したデジタル時計があります。ただし、この時計は24時間表示で、午後3時を15:00と表します。
- (1) 今から1時間の間に、画面のどこかに数字の「9」が出ている時間は何分間ありますか。
- (2) 今から3時間の間に、画面のどこかに数字の「3」が出ている時間は何分間ありますか。

何回でできるかな
- 内容
- 論理
- 思考力
- 筋道を立てて考える力
3本のカギにそれぞれ対応する3個の錠前があります。しかし、どのカギがどの錠前のものかわかりません。カギを錠前に差し込んでカギが開くかどうかという操作を少なくとも何回ためせば、どのカギがどの錠前のものかわかりますか。

答えと考え方
線でむすぼう
答え
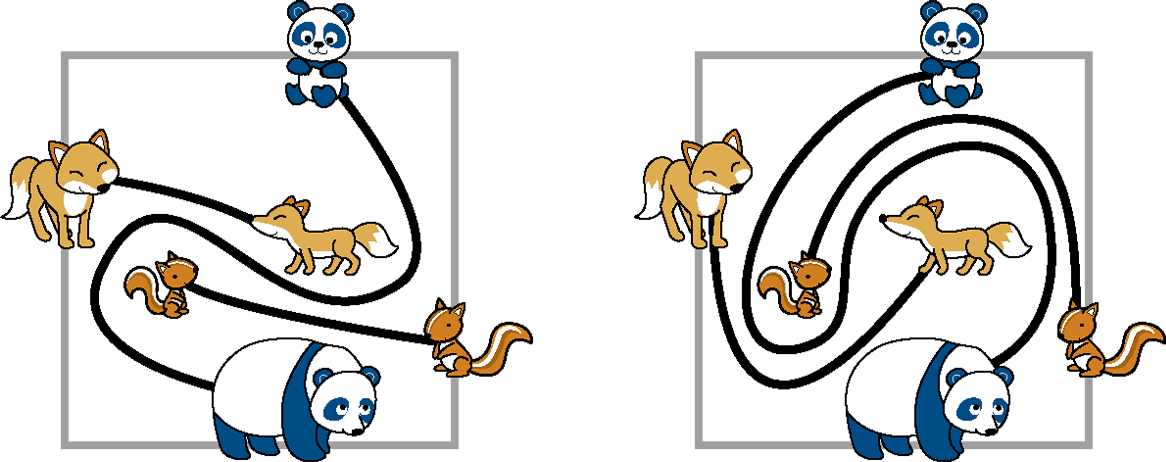
ほかにもあるか、さがしてみよう。
考え方
最初にパンダをまっすぐむすぶと、キツネもリスもむすべません。ですので、最初にキツネとリスをむすびます。そして、その線の間をぬうように、パンダをむすびます。
重なっている順番
答え
赤→青→茶→黒→白→黄
考え方
じゃんけん
答え
考え方
1人だけ勝つ場合、2人が勝つ場合、あいこになる場合を、1回目、2回目、3回目の場合に分けて考えます。
たとえば、1回目を「1人だけ勝つ場合」にすると、たくみさんがグーを出しているので、ともこさんがチョキになります。続いて2回目を「2人が勝つ場合」にすると、なおみさんにはチョキが入ります。そして3回目は「あいこになる場合」とすると、たくみさんにパーが入ります。
最後に勝った回数をたしかめると、たくみさんは1回目に勝ち、なおみさんとともこさんは2回目に勝ち、それぞれ1回ずつ勝ったので、正しいと言えます。

また、もし2回目を「あいこになる場合」とすると、なおみさんはグーとなりますが、3回目になおみさんとともこさんの2人が勝つようにはできないので、まちがいとなります。
ほかの答えも、同じように考えます。
カレンダー
答え
(1) 4月 (2) 水曜日
考え方
- (1) 1週間は7日なので、日数を7でわったときに、あまりがなければ前の曜日、あまりが1ならば同じ曜日、あまりが2ならば次の曜日…のようになります。
2月1日は、(31+1)÷7=4あまり4 より、日曜日
3月1日は、(29+1)÷7=4あまり2 より、月曜日
4 月1 日は、(31+1)÷7=4あまり4 より、木曜日
ですから、次に1日が木曜日になるのは4月です。 - (2) 1月1日から5月5日までの合計日数を求めると、
31+29+31+30+5=126(日) となります。
(1)と同じように求めると、126÷7=18 より、水曜日とわかります。
展開図
答え
考え方
- (1) 「さ→ん→す→う」とならべるためには、最初に書かれている「う」の左どなりに「す」を置きます。「す」の左どなりに「ん」がくるので、「う」の右どなりに「さ」、「さ」の右どなりに「ん」がきます。
- (2) 「う」の反対側の面に「ん」がきます。このとき、向きに注意します。「ん」の右どなりが「す」です。「う」の右どなりに「さ」がきます。このとき、向きに注意します。
◯に数を入れよう
答え
(1) 15、30
(2) 9個
(3) 16個
考え方
- (1) アには、3と5の両方でわることができる数字(3と5の公倍数)が入ります。
- (2) イには、2と5の両方でわることができる数字(2と5の公倍数)が入ります。2と5の最小公倍数は10なので、イには10の倍数が入ります。10の倍数のうち2けたの自然数は、10、20、30、40、50、60、70、80、90の9個です。
- (3) ウには、2でわることができる数字(2の倍数)が入ります。エに「最大で何個の100以下の自然数が入るか」を求めるので、ウには2の倍数のうちいちばん小さい2を入れます。すると、エには、2と3の両方でわることができる数字(2と3の公倍数)が入ることがわかります。2と3の最小公倍数は6なので、エには100以下の6の倍数が入ります。100以下の6の倍数は、6、12、18、24、30、36、42、48、54、60、66、72、78、84、90、96の16個です。
デジタル時計
答え
(1) 6分間 (2) 90分間
考え方
- (1) 今、11:00を示している時計は、1時間後には12:00を示す。この1時間の間に画面のどこかに数字の「9」が出ているのは、
・11:09 を示している1分間
・11:19 を示している1分間
・11:29 を示している1分間
・11:39 を示している1分間
・11:49 を示している1分間
・11:59 を示している1分間
だから、全部で6分間ある。 - (2) 今、11:00を示している時計は、3時間後には14:00を示す。この3時間の間に画面のどこかに数字の「3」が出ているのは、11:00〜11:59では、
・11:03 を示している1分間
・11:13 を示している1分間
・11:23 を示している1分間
・11:30〜11:39 を示している10分間
・11:43 を示している1分間
・11:53 を示している1分間
だから、15分間ある。
12:00〜12:59でも同様である。
13:00からの1時間は、画面のどこかにずっと数字の「3」が出ている。
よって、全部で、15×2+60=90(分間)
何回でできるかな
答え
3回
考え方
3個の錠前をそれぞれA・B・C、3本のカギをそれぞれa・b・cとする。
まず、A─a、A─bの2回ためせば、Aの錠前に合うカギがわかる。次に、残りの2本のカギのうち1本をBの錠前にためせば、1回でBの錠前に合うカギがわかる。
残ったものがCの錠前に合うカギだから、 2+1=3(回)

