TOPICS

2025年度 第１回のふり返り、今回は３級の問題です。

【問題】
下の図のように、縦12cm、横５cmの長方形の紙を、のりしろ（図のかげのついた部分）の幅をすべて１cm にして、重ねて貼り合わせます。貼り合わせる長方形の紙の枚数がもっとも少ないとき、正方形の面積を求めなさい。

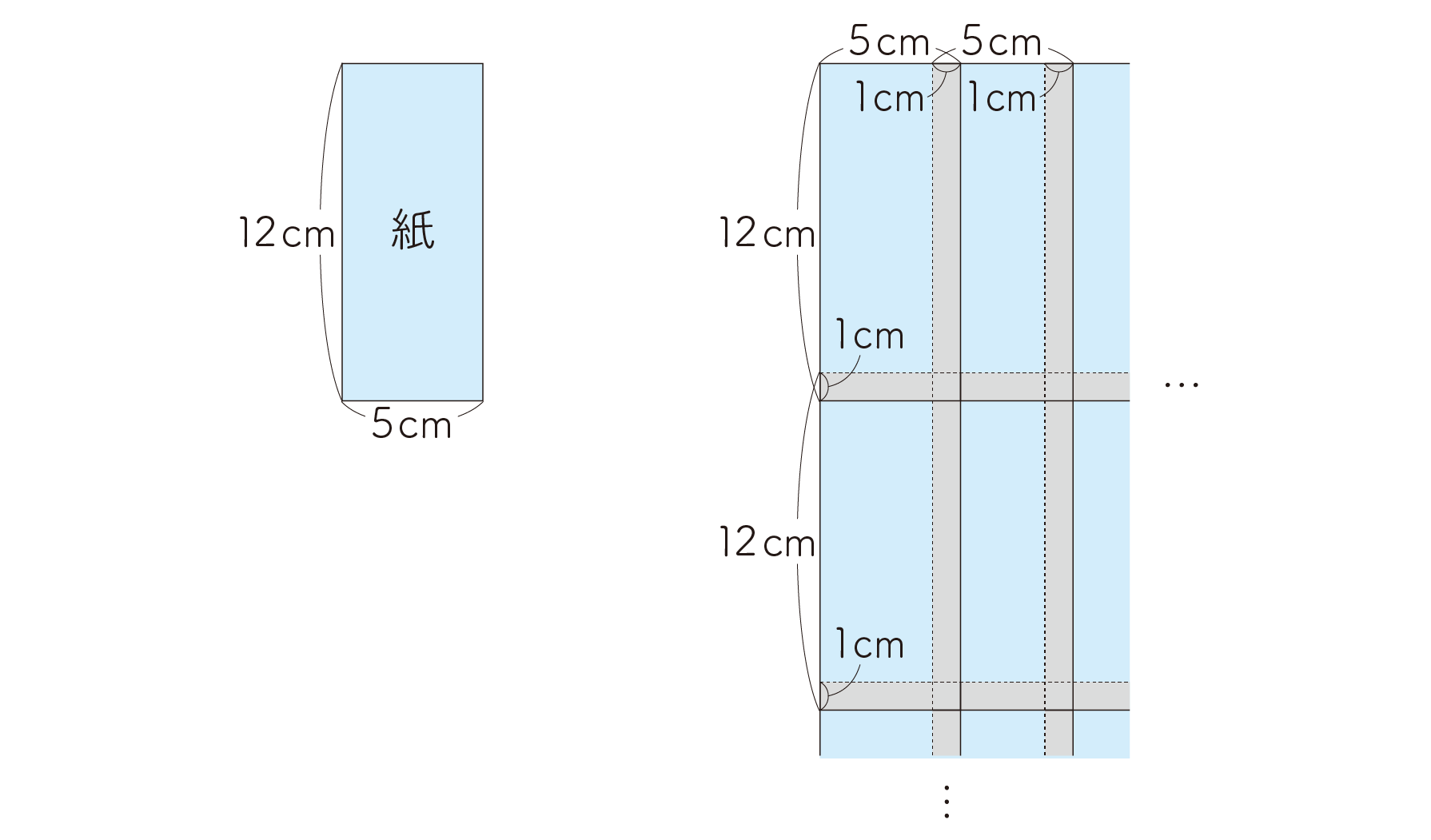
【考え方】
長方形の紙を縦にｍ枚，横にｎ枚貼り合わせると、
縦の長さは、12＋11(m−1)＝11m＋1(cm)
横の長さは、5＋4(n−1)＝4n＋1(cm)
となります。
正方形になるとき、縦と横の長さは等しいから、
　　11m＋1＝4n＋1 より、11m＝4n
11と４の最小公倍数は 11×4 だから、これを満たすもっとも小さいｍ、ｎは、
m＝4、n＝11 となります。
このとき、正方形の辺の長さは、11×4＋1＝45(cm) だから、
正方形の面積は、45×45＝2025(㎠) となります。

３級なので文字式で解説しましたが、11と４の最小公倍数を考える問題だと思えば、小学生でも解けます。（最小公倍数は小５で学習します）
また、最小公倍数を知らなくても、縦は11ずつ増えていき、横は４ずつ増えていくという変化を捉えて、同じ値になるものを探せばよいということに気づけば解けるので、もっと低学年の子でも考えられる問題です。

　縦：11、22、33、44
　横：4、8、12、16、20、24、28、32、36、40、44

このように小学生でも考えられる問題ですが、正答率は28.4％と低迷しました。

この問題の前の小問が『長方形の紙を縦にｍ枚、横にｎ枚貼り合わせて長方形をつくります。このとき、長方形の周りの長さを、ｍ、ｎを使って表し、計算しなさい。また、考え方も書きなさい。』という問題だったため、数学的に文字式を使って考えなければ解けないのではないかと考え、苦労した可能性もあります。実際、無回答者は27.2％もいました。

なお、誤答の解答類型ですが、偏った傾向はなく、バラバラでした。
ただ、正方形の面積を求める問題なので、何かの数の平方数（２乗した数）が答えになると想像して欲しいところですが、平方数を答えた割合は14.8％だったのに対し、平方数以外を答えた割合は19.8％と、後者の反応率のほうが高く出ました。

●まとめ●
小学生でも考えられる問題であったため、もし６級〜８級でこの問題を単体で出題したら、もっと高い正答率になったかもしれません。３級だからといって難しく構えず、柔軟に発想する習慣が必要ですね。