TOPICS

2025年度 第１回のふり返り、今回は４級の問題です。

【問題】
下の図のような、▶と◀の間に決まった４つの数字を合わせてはずす鍵があります。Ａ、Ｂ、Ｃ、Ｄにはそれぞれ10個の面があり、０から９の数字が１つずつ書かれています。

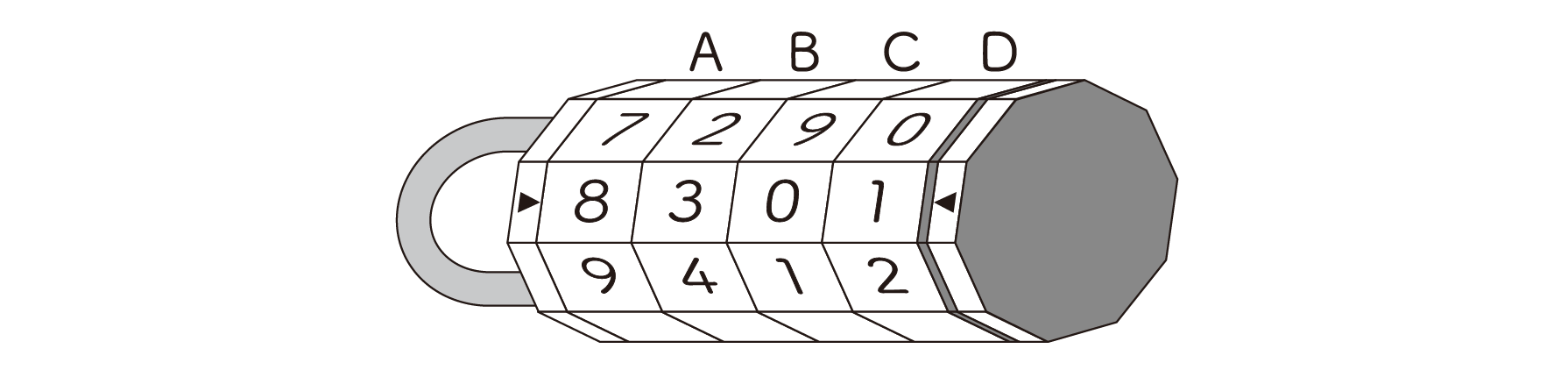
孝平さんは、この鍵をはずす番号を忘れてしまいました。しかし、念のため鍵をはずす番号のヒントをメモしておいたので、それをもとに考えることにしました。

しかし、鍵をはずす番号のヒントが書かれたメモには、もう１つヒントを加えないと番号がわかりません。次の(ア)から(エ)の中に１つだけ鍵をはずす番号を特定できる条件があります。それはどれですか。また、鍵をはずす番号も答えなさい。

(ア)　ＡとＢの数はどちらも奇数である。
(イ)　Ａの数からＢの数をひくと３になる。
(ウ)　Ｂの数はＡの数でわり切れる。
(エ)　Ａの数は偶数である。

【考え方】
ヒントの条件ではＡとＢの数が絞り切れないので、まずはＣとＤの数を求めます。
ヒント①から、A＋B と C＋D は、12、15、18のいずれかです。

・A＋B＝C＋D＝12 のとき
　ヒント②より A＋B＋D＝12＋D＝18 となり、D＝6 となります。
　このとき、C＋D＝12 より C＝6 となるので、条件を満たします。
・A＋B＝C＋D＝15 のとき
　ヒント②より A＋B＋D＝15＋D＝18 となり、D＝3 となります。
　このとき、C＋D＝15 よりC＝12 となるので、条件を満たしません。
・A＋B＝C＋D＝18 のとき
　A＝B＝C＝D＝9 となるので、ヒント③を満たしません。

よって、C＝D＝6 です。

次に、ヒント④ と C＝D＝6 より B＞6 となり、A＋B＝12 から、ＡとＢは次の３通りが考えられます。
　　A＝3、B＝9　／　A＝4、B＝8　／　A＝5、B＝7
あとは、ＡとＢを１つに特定できるような条件さえあれば番号が決まります。

・(ア)の場合
　A＝3、B＝9 と A＝5、B＝7 が考えられ、１つに特定できません。
・(イ)の場合
　A−(12−A)＝3 より、A＝7.5 となり整数ではないので、条件を満たしません。
・(ウ)の場合
　A＝3、B＝9 と A＝4、B＝8 が考えられ、１つに特定できません。
・(エ)の場合
　Ａが偶数になるのは、A＝4、B＝8 のときだけなので、１つに特定できます。

よって、鍵をはずす番号は 4866 となります。

正答率は14.0％と、かなり低い数値を示しました。まずは、番号について、解答類型とその反応率を見てみましょう。

4866：28.0％　　3966：20.0％　　5766：14.0％
その他：24.0％　　無回答：14.0％

また、4866と答えた生徒28％の選択肢(ア)～(エ)の反応率は、次の通りです。
(ア)：0.0％　　(イ)：2.0％　　(ウ)：12.0％　　(エ)：14.0％

4866、3966、5766が上位３つを占めたことからも、C＝D＝6 は多くの生徒が分かっています。ちなみに、この３つの答え以外も含めて C＝D＝6 が分かった生徒の割合は66.0％でした。

また、上位３つの答え 4866、3966、5766 を見ると、ヒント①～④のすべての条件を満たしているので、62.0％の生徒は、この３つに絞り込めたのだと思われます。

あとは、この３つから１つに絞り込むための条件を(ア)～(エ)から選ぶのですが、その過程で半分の生徒がつまずきました。

●まとめ●
この問題は中学生を対象としていますが、複雑な計算を必要としないため、小学生でも十分に考えられる問題です。重要なのは、与えられた条件を丁寧に読み取り、矛盾のない組み合わせを順に絞り込んでいくことです。さらに、追加条件によって一つに特定していく——その過程に、情報を整理し、筋道を立てて考える力が問われます。
年齢にかかわらず、「条件を一つずつ確かめ、比較しながら除外していく」思考の流れを身につけることが大切です。