TOPICS

2025年度 第１回のふり返り、今回は６級の問題です。

【問題】
山根さん、川本さん、海野さんの３人が店で働くことになりました。３人は、12月１日から同時に働き始めますが、12月31日までの１か月間の働き方はそれぞれちがい、
　山根さん…２日間続けて働いて１日休み
　川本さん…３日間続けて働いて２日間続けて休み
　海野さん…５日間続けて働いて３日間続けて休み
をくり返します。
２回目に３人が同時に休みになるのは、12月何日ですか。

【考え方】
働く日を○、休む日を×とすると、次のような表に
なります。

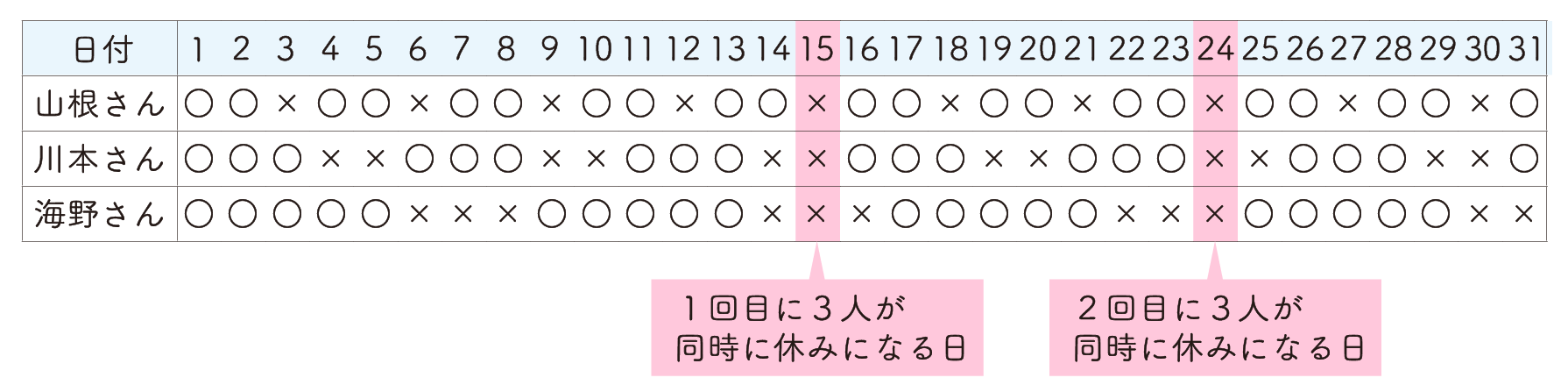
よって、３人が同時に休みになるのは、１回目が12月15日、２回目が12月24日です。

正答率は40.4％で、解答類型とその反応率は次の通りです。

12月15日：21.7％　　12月30日：13.9％　　12月14日：3.0％
12月11日：1.9％　　12月12日：1.9％　　12月６日：1.5％
12月23日：1.5％　　12月21日：1.1％　　12月22日：1.1％
12月26日：1.1％　　12月29日：1.1％　　その他：6.1％
無回答：3.7％

最も多い12月15日は、１回目に３人が同時に休みになる日を答えたのでしょう。
次に多い12月30日は、１回目が15日だったので、その倍である30日と考えたのだと思われます。

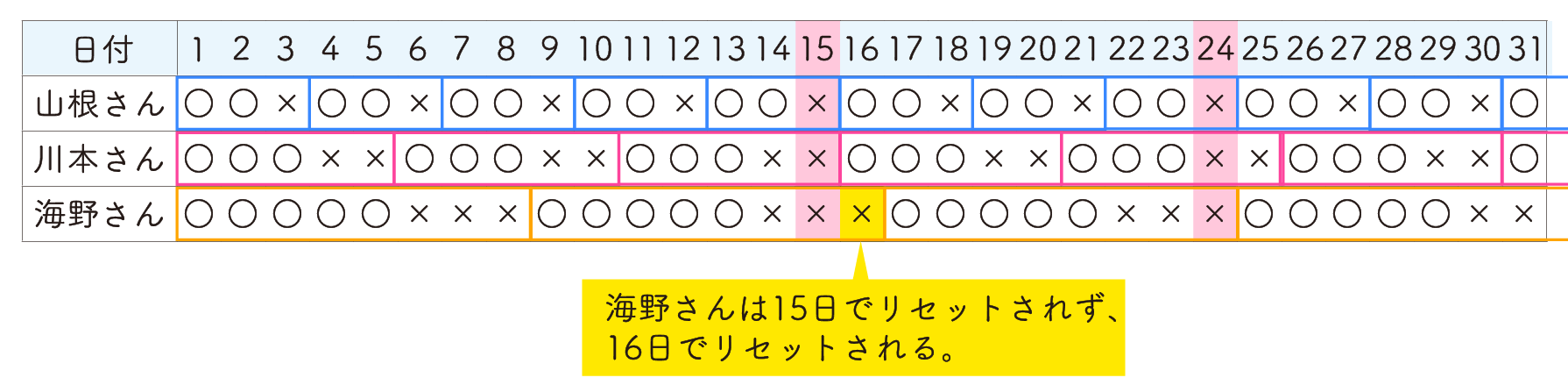
表を改めてよく見ると、山根さんと川本さんは、15日が連続する休みの最終日になっていますが、海野さんは３連休のうちの２日目なので、まだ休みが１日余っています。これに気づかず、海野さんも含めて15日でリセットさせてしまったことで、30日という間違いにつながりました。

●過去との比較●
では、過去に出した類題と比較してみましょう。
過去に出した類題は、次の通りです。

【問題】
松井さん、竹田さん、梅野さんの３人が交代でうさぎのえさやり当番をすることになりました。３人は、１月１日から当番を始めますが、３人は、
　松井さん…２日間続けてえさやりをして１日休み
　竹田さん…５日間続けてえさやりをして１日休み
　梅野さん…８日間続けてえさやりをして１日休み
をくり返します。
２月に初めて３人が同時に休みになるのは、２月何日ですか。

今回の問題と違うのは、休みが３人とも１日というところです。
つまり、同時に休みになる日を考えるには、最小公倍数を考えればよいということです。休みを含めた日数を１まとまりとすると、松井さんは３日、竹田さんは６日、梅野さんは９日で１まとまりとなります。よって、３と６と９の最小公倍数である18日に１回、３人が同時に休みになります。

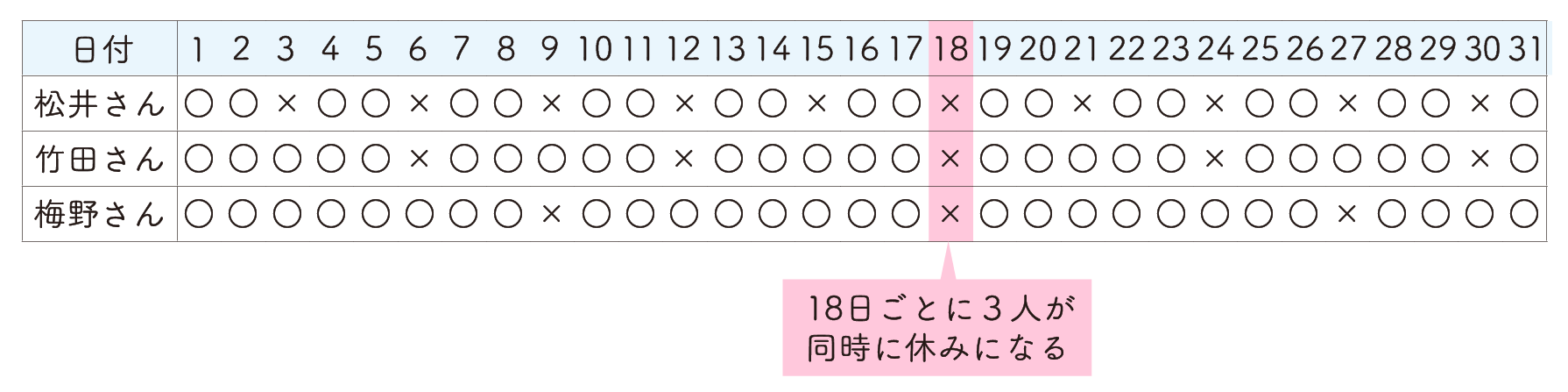
つまり、１月18日に３人が同時に休みになり、次に３人が同時に休みになるのはその18日後なので、18×2＝36、かつ１月は31日までなので、36−31＝5 より、２月５日となります。

この問題の正答率は42.7％で、今回とほぼ同じでした。また、解答類型とその反応率は次の通りです。

２月18日：9.8％　　２月６日：5.8％　　２月９日：4.7％
２月10日：4.7％　　２月17日：3.6％　　２月４日：3.3％
２月24日：2.9％　　２月23日：2.5％　　２月３日：2.2％
２月13日：1.8％　　２月16日：1.8％　　２月14日：1.4％
その他：6.6％　　無回答：6.2％

最も多かった２月18日は、１月末でリセットし、２月１日から再びルールを適用したものです。月が変わるとルールがリセットされると問題文には記されていないのに、ルールをリセットする、または毎月１日から同じルールが適用されると考える子は一定数いるようです。

次に多かった６日は、おそらく１月を30日までとして計算したのでしょう。

９日と10日は、休みを含まない２・５・８の最小公倍数「40」で考えた可能性があります。（40−31＝9、または40−30＝10）

●まとめ●
今回の問題では、周期のとらえ方を誤り、１回目に全員が休んだ日を「周期のはじまり」として計算してしまう誤答や、「月が変わるとリセットされる」といった、問題文に書かれていないルールを勝手に適用してしまうケースが多く見られました。

このようなミスをする子どもには、「頭の中だけで考えてしまう」という傾向がよくあります。ルールを正確に読み取り、筋道を立てて考えるためには、まず表や図を使って情報を整理させることが効果的です。

計算力だけでなく、「書き出して考える習慣」を身につけることで、問題の構造を正しくとらえ、正解にたどりつく力を伸ばすことができます。