TOPICS

2025年度 第１回のふり返り、今回は８級の問題です。

【問題】
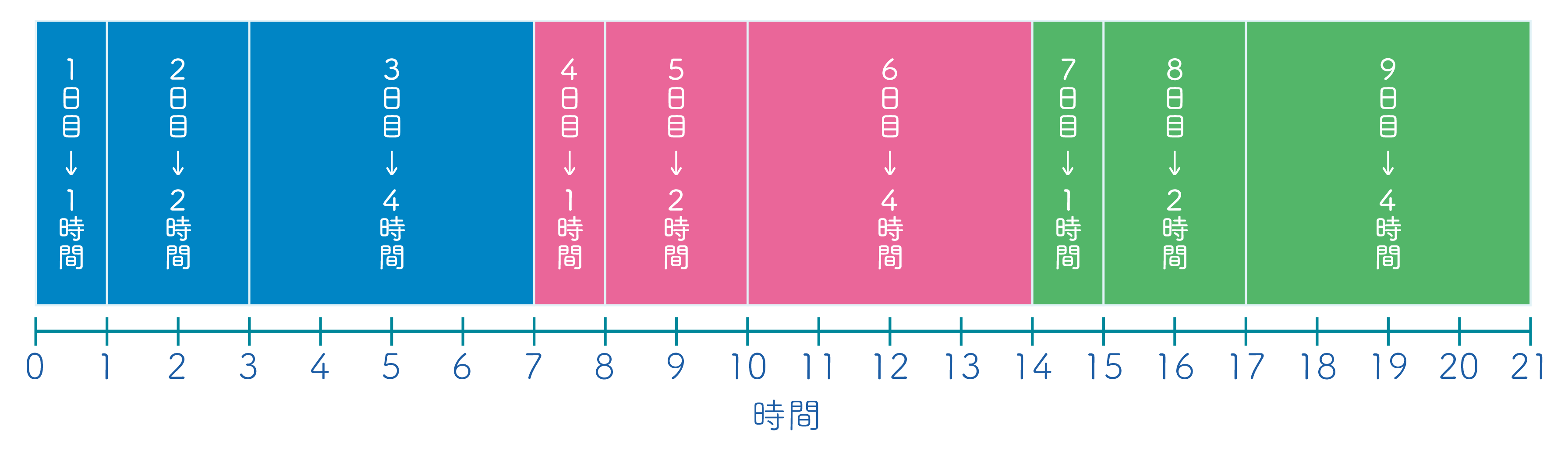
なぎささんは、10日間の中で読書を20時間することにしました。
(1)　なぎささんは、１日目は１時間、２日目は１日目の２倍、３日目は２日目の２倍の時間、読書をすることにしました。このとき、なぎささんの３日目までの読書の時間の合計は何時間ですか。
(2)　なぎささんは、(1)のように読書をしたあと、４日目からは、１日目から３日目までの時間をくり返すように読書をすることにしました。なぎささんが合計20時間の読書をしたことになるのは何日目ですか。

【考え方】
(1)　１日目から３日目までの読書時間は、次の通りです。
　　１日目：１時間
　　２日目：１日目の２倍なので２時間
　　３日目：２日目の２倍なので４時間
　よって、３日目までの合計は、1＋2＋4＝7時間
(2)　３日間で７時間なので、６日間では 7×2＝14時間 となります。
　７日目は１時間にもどるので、
　　７日目：14＋1＝15時間
　　８日目：15＋2＝17時間
　　９日目：17＋4＝21時間
　となり、合計20時間になるのは９日目とわかります。

正答率は、(1)63.5％、(2)40.5％でした。
また、解答類型とその反応率は、次の通りでした。

(1)　４時間：12.7％、６時間：8.4％、９時間：7.1％、５時間：2.3％
　　 ８時間：1.5％、10時間：1.3％、３時間：1.0％、12時間：0.8％
　　 その他：1.1％、無回答：0.3％
(2)　６日目：10.6％、５日目：9.9％、８日目：9.6％、７日目：5.1％
　　 ３日目：3.5％、４日目：3.3％、11日目：3.3％、12日目：3.3％
　　 15日目：2.5％、10日目：2.0％、14日目：1.0％、その他：3.4%
　　 無回答：2.0％

(1)の誤答分析
４時間（12.7％）
⇒問題文を「３日目は何時間ですか？」と読み間違え、３日目の時間を答えたものと思われます。

６時間（8.4％）
⇒ 1＋2＋3＝6 と計算したものと思われます。「１時間ずつ増えた」と誤認し、２日目を 1＋1＝2、３日目を2＋1＝3とした可能性が考えられます。

９時間（7.1％）
⇒ 1＋3＋5＝9 と計算したものと思われます。「２時間ずつ増えた」と誤認し、２日目を 1＋2＝3、３日目を 3＋2＝5 とした可能性が考えられます。

５時間（2.3％）
⇒ 1＋2＋2＝5 と計算したものと思われます。「３日目を１日目の２倍」と誤認し、２日目も３日目も 1×2＝2 とした可能性が考えられます。

(2)の誤答分析の前に、(1)と(2)を合わせた解答類型と反応率を見てみましょう。
４時間・５日目：2.8％、４時間・６日目：2.3％、４時間・８日目：1.5％
４時間・９日目：2.0％、４時間・15日目：1.8％
６時間・６日目：1.3％、６時間・11日目：1.8％、６時間・12日目：2.0％
７時間・３日目：2.8％、７時間・４日目：1.0％、７時間・５日目：5.6％
７時間・６日目：3.5％、７時間・７日目：2.0％、７時間・８日目：4.3％
７時間・９日目：37.7％（どちらも正解）、７時間・11日目：1.3％
９時間・７日目：1.3％、９時間・８日目：3.0％
10時間・６日目：1.0％、その他：21.0％

(1)・(2)ともに正解した子が37.7％だったので、(1)で正解した子の中でも約60％しか(2)を正解していない計算になります（0.377÷0.635≒59.4％）。

また、４時間・９日目と答えた子（2.0％）は、(1)は３日目の４時間を答え、かつ(2)は正解しています。問題文を適切に読んでいれば、(1)も正解できたでしょう。

(2)の誤答分析
６日目（10.6％）
⇒(1)を正解した７時間の子（3.5％）は、「３日目７時間＋６日目14時間＝21時間」で、「20時間≒６日目」と勘違いした可能性があります。
⇒(1)で３日目の４時間を答えた子（2.3％）は、３日間で７時間がわかっていると思われます。そのうえで、７時間を３倍すると21時間になって20時間を超えるので、７時間を２回くり返した６日目と考えた可能性があります。
⇒(1)で６時間と答えた子（1.3％）は、1＋2＋3＋…と考えている可能性があるので、1＋2＋3＋4＋5＋6＝21時間 より、６日目と考えたと思われます。

５日目（9.9％）
⇒(1)を正解した７時間の子（5.6％）が４日目以降も２倍ずつ読書時間が増えてくと捉えたと想像すると、４日目が３日目の２倍＝８時間、５日目が４日目の２倍＝16時間となるので、1＋2＋4＋8＝15時間、1＋2＋4＋8＋16＝31時間 から５日目と判断したのかもしれません。
⇒(1)で３日目の４時間と答えた子（2.8％）も同様の可能性があります。

８日目（9.6％）
⇒(1)を正解した７時間の子（4.3％）は、９日目までを合計すると 1＋2＋4＋1＋2＋4＋1＋2＋4＝21時間となり20時間を超えるので、１日引いて８日目とした可能性があります。
⇒(1)で３日目の４時間を答えた子（1.5％）も同様だと思われます。
⇒(1)で９時間と答えた子（3.0％）は、1＋2＋5＋1＋2＋5＋1＋2＝19時間、1＋2＋5＋1＋2＋5＋1＋2＋5＝24時間より、９日目と答えられそうな気もしますが、９日目では20時間を大きく超えるので、８日目としたのかもしれません。なお、９時間・９日目と答えた子は１人もいませんでした。

７日目（5.1％）
⇒(1)を正解した７時間の子（2.0％）は、７日目を７時間と誤変換し、６日目までの7＋7＝14時間に７日目の７時間を足して21時間としたのでしょうか。少し強引な推測かもしれませんが。
⇒(1)で９時間と答えた子（1.3％）も同様に７日目＝７時間とすると、8＋8＋7＝23時間より、７日目と考えることもできます。やはり、強引な推測ですが…。


なお、過去にこの問題を出題したときは、(1)が「１週間の合計時間」、(2)が「60時間になるのは何日目か」という問題でした。そのときの正答率は、(1)が50.6％、(2)が8.3％でした。積み上げる数値（時間・日数）が大き過ぎた影響で正答率がかなり低く出たため、今回は前回よりも数値を小さくしました。結果として正答率は上がりましたが、それでも条件設定を適切に読み取れずに間違える子が一定数いることが見てとれました。

●まとめ●
今回の結果から、(1)では「倍にしていく数の変化」を正しく捉えられなかったり、(2)では「積み上げていく過程を1日ずつ丁寧に追う」ことができなかったりする姿が見えてきました。数の大きさや繰り返しの構造を扱う際には、途中経過を表や図にして確かめることが効果的です。
こうした傾向は、単なる計算力だけでなく「どのように状況を整理し、見通しを持って考えを進めるか」という思考の姿勢に直結しており、今後の学習において重要な示唆を与えるものと言えるでしょう。