TOPICS

2024年度 第３回のふり返り、今回は３級の問題です。

３級の第３回は飛び級で受ける子が多く、さらに飛び級で受ける子は優秀な子が多いため正答率が高くなる傾向があるのですが、この問題は正答率が低く出ました。
対象級より低学年でも考えれば解ける問題ではありますが、それでも思考するのが少し難しい問題といえます。

【問題】
池のまわりの遊歩道を、ＡさんとＢさんがスタート地点から同時にスタートして、１周します。遊歩道の１周は960mで、Ａさんは毎分80m、Ｂさんは毎分160mで同じ方向に進みます。また、先に１周した人は、相手がスタート地点に戻ってくるまで待ちます。２人が同時に出発してからｘ分後の２人の間の道のりをｙmとするとき、ｘとｙの関係を表すおよそのグラフをかきなさい。

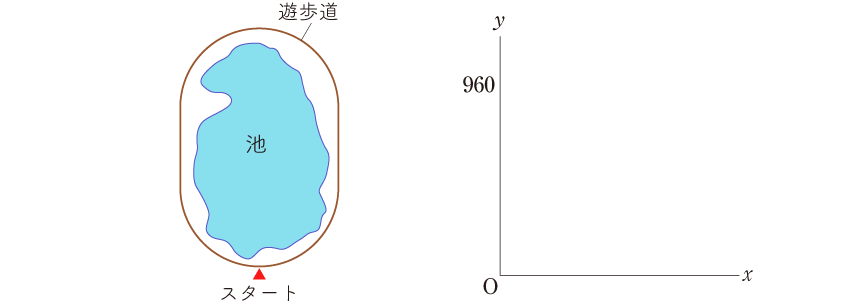
【考え方】
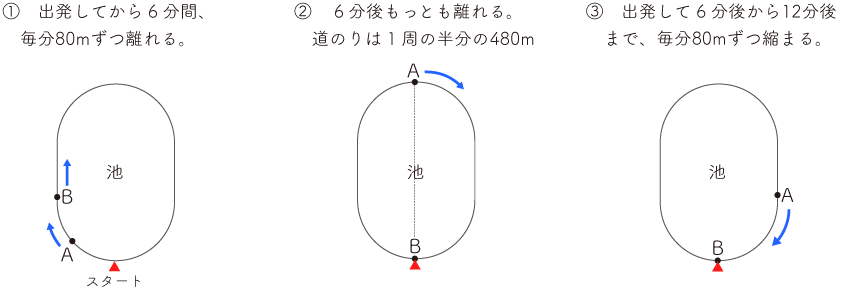
２人の間の道のりは、毎分
　　160－80＝80（m）
ずつ離れます。（下の図①）
また、Ｂさんは１周するのに、
　　960÷180＝6（分）
かかるので、もっとも離れるのは、Ｂさんがスタート地点に戻る６分後となります。（下の図②）
また、Ａさんが１周するのに、
　　960÷80＝12（分）
かかるので、２人が同時に出発して６分後から12分後までは、２人の間の道のりは毎分80mずつ縮まり、12分後には０になります。（下の図③）

これをグラフに表すと、次のようになります。

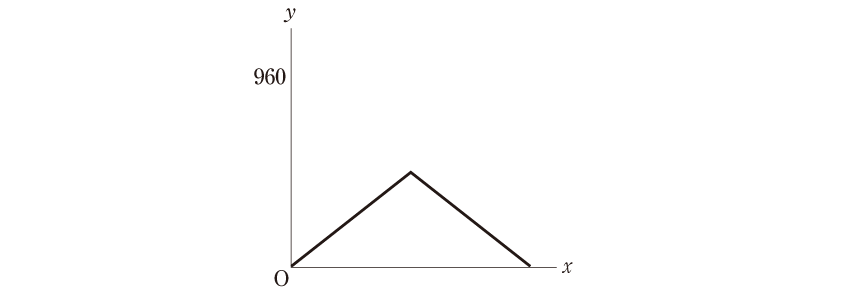
正答率は、30.4％でした。

ポイントは、左右対称であることと、頂点が480mのあたりであることです。

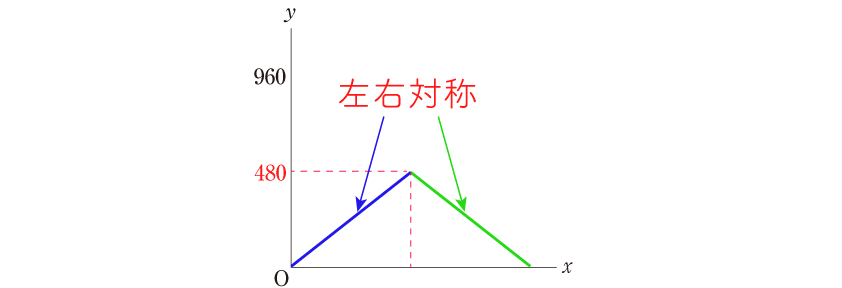
このどちらか、または両方が正しく描けていなかったものが目立ち、全体の34.8％もいました。
このことから、だんだん広がっていき、そしてだんだん狭くなっていくということまではイメージできているのに、数量的な部分をイメージできていない子が多いことがわかります。

一方で、比例のグラフを描いた子が30.4％もいました。だんだん２人の間が広がっていくということはイメージできても、Ｂさんが先に着いたあとに距離が縮まっていくというイメージができなかったのでしょう。

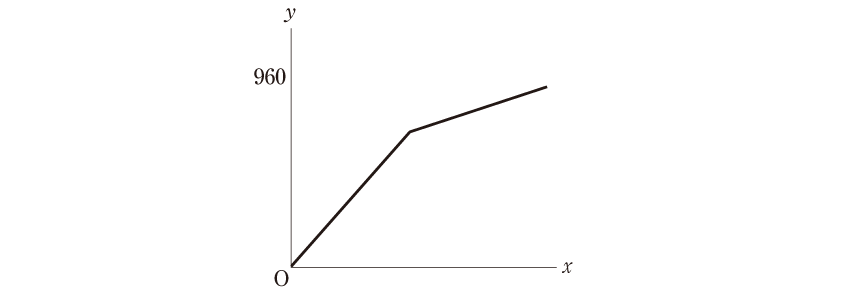
また、次の図のように、途中でグラフの傾きを緩やかにした子もいました。（4.3％）
この子は、Ｂさんが先に着いたあとに変化が起こるというイメージまでは浮かんだのでしょう。

この問題のように、数量的なデータから変化を読み取り、グラフをイメージする力はとても重要です。日常生活の場面でも、メディアなどで取り上げられているグラフを誤読している場面をよく見かけますので、大人になってもとても必要な力です。

データを正しく読み、そしてそのデータからどのようなグラフができそうかというイメージを作る練習はとても重要なので、繰り返し練習するとよいでしょう。