TOPICS

2024年度 第３回のふり返り、今回は４級の問題です。

数値だけで示されていればもう少し正答率が高くなったと思うのですが、文字が入るだけで戸惑いが生まれて解けなくなってしまったのかなという問題です。

【問題】
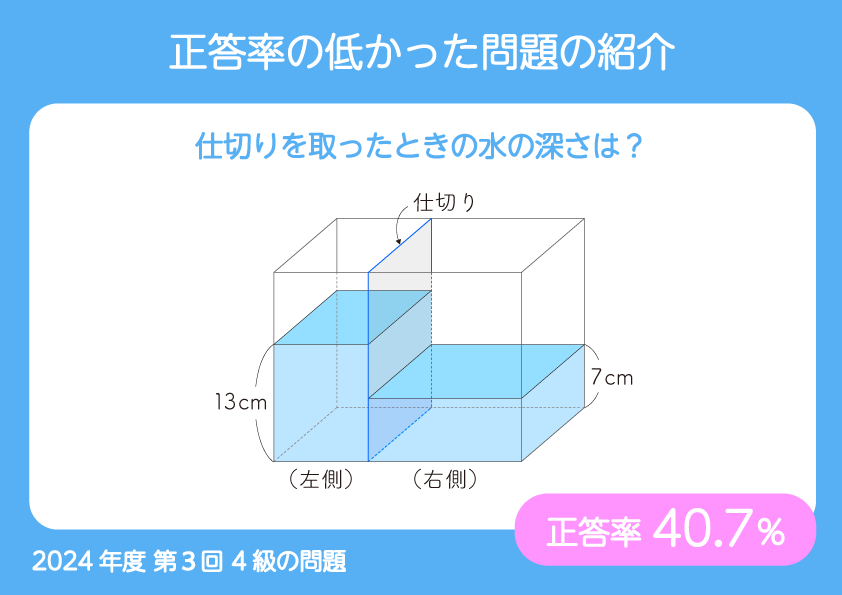
図のような直方体の容器があります。容器の内側には水を通さない仕切りがついていて、仕切りの左側と右側には、それぞれ同じ量の水が入っています。仕切りの左側と右側はどちらも直方体です。仕切りの左側の底面積を 7a ㎠ とするとき、次の問いに答えなさい。
(1)　仕切りの右側の底面積を a を使った式で表しなさい。
(2)　仕切りを取ったときの水の深さを求めなさい。

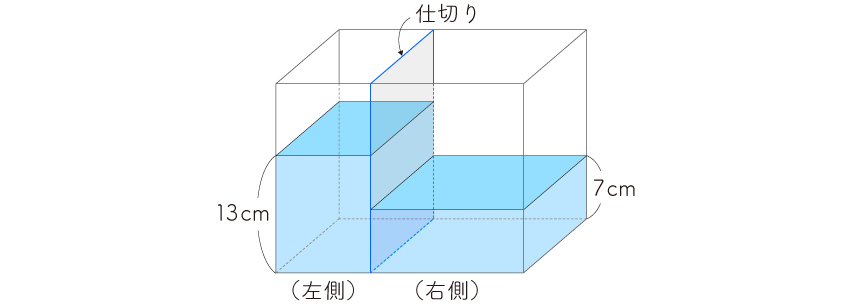
【考え方】
(1)左側の水の体積は、
　　7a×13＝91a（㎤）
　左側と右側の水の量は同じなので、右側の底面積は、
　　91a÷7＝13a（㎠）
　となります。

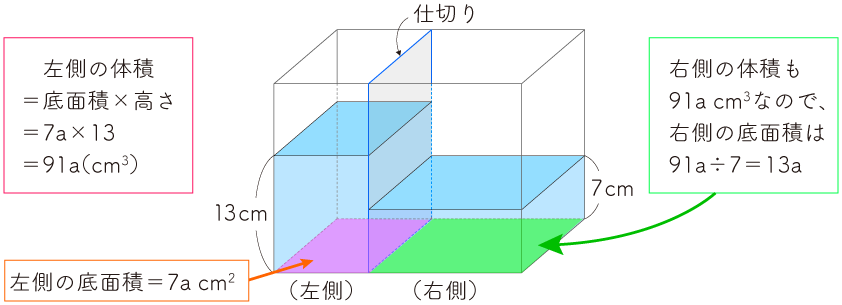
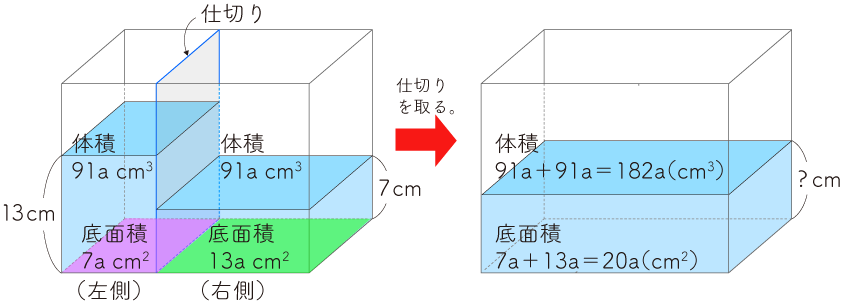
(2)容器に入っている全部の水の体積は、
　　91a＋91a＝182a（㎤）
　これを全体の底面積 7a＋13a＝20a（㎠）でわると、
　　182a÷20a＝9.1（㎝）
　となります。

正答率は、(1)が61.1％、(2)が40.7％でした。

(1)は「体積÷高さ＝底面積」を計算するだけなのですが、最初に左側の体積を求めるステップ（7a×13＝91a）で戸惑ったのかもしれませんし、その次のステップ（91a÷7＝13a）で戸惑ったのかもしれません。
文字式で表すことにまだ慣れていない子が、まだいることが感じられます。

では、(2)の解答類型とその反応率を見てみましょう。
10cm：7.4％　９cm：5.6％　182a cm：3.7％　３cm：3.7％
無回答：25.9％

(2)は「考え方」も記述させる問題だったので、どのように考えて間違えたかも把握できましたので、それを踏まえて子どもたちの思考を見ていきます。

【10cm】
(13＋7)÷2＝10　という求め方と、
13－7＝6　6÷2＝3　13－3＝10　7＋3＝10　という求め方がありました。
前者は「左側と右側の高さを足して半分にする」という考え方で、後者は「左側と右側の差を出してそれを半分にし、大きいほうからはその値を引き、小さいほうにはその値を足す」という考え方です。
左側と右側で底面積が同じであればこの考え方でもよいのですが、この問題は底面積が左右で違うので、そこを考慮しなければなりません。

【３cm】
上記10cmの、「13－7＝6　6÷2＝3」から３cmと答えていました。10cmと同じように、底面積が違うことを考慮できていません。

【182a cm】
全体の水の体積（91a＋91a＝182a）を答えています。

【９cm】
13－7＝6　6÷3＝2　7＋2＝9　という求め方がありました。
どうして３でわったのかはわかりません。

ほかには、左側のほうが 7a×(13－7)＝42a ㎤ 体積が大きく、これを全体の底面積13a＋7a＝21a（この足し算も間違えています）でわると、42a÷21a＝2
これを7cmに足して９cm と答えていた子もいました。

差を求めて、それを半分にすればよいのではという思考の形跡は感じられますね。

一方で、無回答が25.9％もいたので、およそ４分の１の子は手が付けられなかったと言えます。

そんな子には、次の図のように、まずは具体的な数値を入れたもので考えさせてみてください。

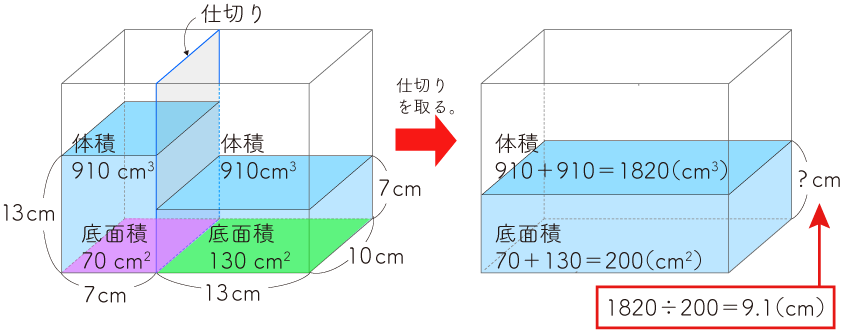
この図は、問題の図の左側の底面積 7a ㎠ を70㎠と置き換え、さらに奥行を10㎝とすることで、底面積を 7㎝×10㎝＝70㎠ と考えられるようにした図です。

このように具体的な数値を入れると、ぐっと考えやすくなると思います。

文字式に慣れていないと、文字式になっただけで同じように考えられなくなる子がいます。そんな子には、このように具体的な数値を入れて考えさせてみるとよいでしょう。