TOPICS

2024年度 第３回のふり返り、今回は５級の問題です。

数を書き出して、そこから必要なものを選んで数えるだけの問題ですが、その条件に合ったものを選ぶのが以外と子どもにとっては難しい。そんな問題です。

【問題】
次のように、１から100までの整数のうち、８の倍数と、 ８の数字をふくむ数（18，81など）を除いたものが、小さい順に並んでいます。
　1，2，3，4，5，6，7，9，10，11，12，13，14，15，17，19，…，100
並んだ整数のうち，６の倍数は何個ありますか。

【考え方】
１から100までの整数のうち、 6 の倍数は次の16個です。
　6，12，18，24，30，36，42，48，54，60，66，72，78，84，90，96
この中から、８の倍数「24，48，72，96」と、８をふくむ数「18，48，78，84」を除くと、次の９個となります。
　6，12，30，36，42，54，60，66，90

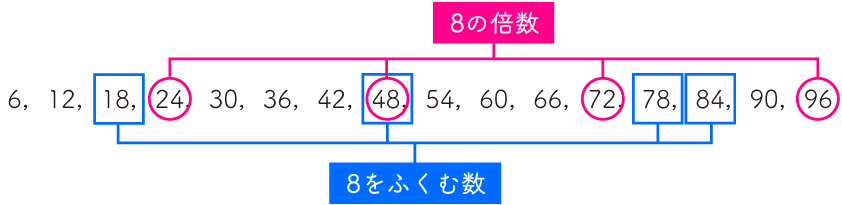
48が「８の倍数」と「８をふくむ数」で重複しているのも注意すべきポイントです。

正答率は21.9％でした。

では、解答類型とその反応率を見てみましょう。
16個：19.0％　８個：11.4％　３個：11.4％　５個：10.5％　10個：9.5％
12個：5.7％　６個：2.9％　４個：1.9％　11個：1.9％　２個：1.9％
13個：1.0％　０個：1.0％

なお、この問題は大問内の(2)なのですが、(1)では「１から50までの整数のうち、並んでいない整数をすべて書きなさい。」という問題を出しました。（正答率は76.2％）
それを踏まえて、各解答類型がどのような考え方をして導き出されたかを想像してみましょう。

【16個】「６の倍数」の個数を答えた。
【８個】48を２回数えてしまい、16－4－4＝８個と考えた。
【５個】(1)の「１から50まで」に引きずられて、6，12，30，36，42を数えた。
【10個】「８の倍数」か「８をふくむ数」のどれかを数え損ねた。または、６の倍数を上げる段階で間違えた。
【12個】「８の倍数」「８をふくむ数」のどちらかのみを引いた。（16－4＝12）
【３個】(1)の「１から50まで」と「並んでいない整数」に引きずられて、６の倍数から「８の倍数」と「８をふくむ数」の18，24，48を数えた。

ここで考えておきたいのは【10個】で想像した『「８の倍数」か「８をふくむ数」のどれかを数え損ねた。または、６の倍数を上げる段階で間違えた。』です。

本当にこのように考え間違えたのかどうかはわかりませんが、九九の範囲を超えた数の中から６の倍数や８の倍数を上げるところで間違える子は一定数いるでしょう。

何の倍数かを判定する方法もありますが、今回はそれを使わずに子どもの立場に立って、考えやすい「６の倍数と８の倍数を導き出し方」を考えてみましょう。

たとえば次のように、60に６の段を足したり、80に８の段を足したりしてはどうでしょうか。やっていることは、60＋6＝66、66＋6＝72、72＋6＝78、…と同じですが、60＋6＝66、60＋12＝72、60＋18＝78、…のほうが、計算ミスをしにくいでしょう。

逆に考えると、たとえば96が６や８の倍数かどうか判断したいときに、96から60や80を引くと、96－60＝36から「36が６の段なので６の倍数である」ことがすぐにわかりますし、96－80＝16から「16が８の段なので８の段である」こともわかります。

このように考えられたら、数え上げ漏れや計算ミスが減って、もう少し正答率が上がったかもしれませんね。
このように考えることも思考力の一つですので、他の段についても、ぜひ考えてみてください。