TOPICS

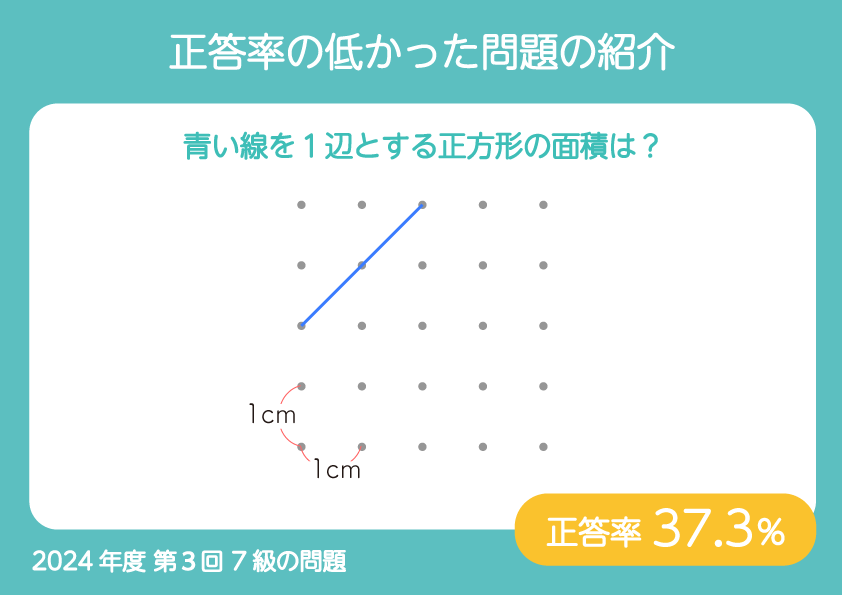
2024年度 第３回のふり返り、今回は７級の問題です。

想定以上に正答率が低くなりましたが、解答類型を見ると子どもたちの思考の癖がよくわかります。

【問題】
縦、横１cmの間隔で並んでいる点があり、これらを結んでいろいろな大きさの正方形をつくります。図１の青い線を１辺とする正方形をつくると図２のようになり、その面積は２㎠です。
(1)(2)の青い線を１辺とする正方形をつくると，その面積はそれぞれ何㎠になりますか。

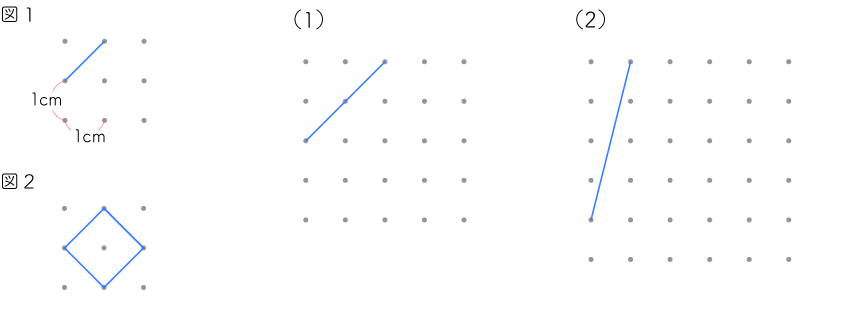
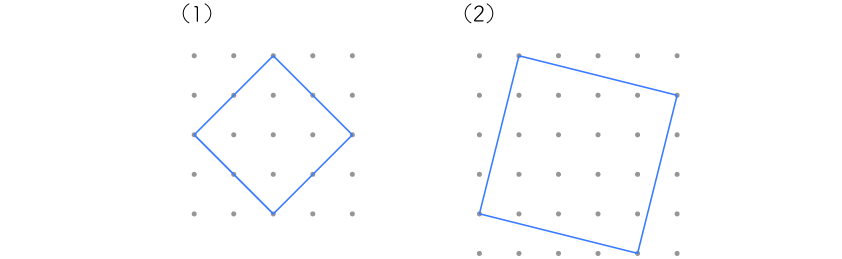
【考え方】
(1)と(2)の正方形は、次のようになります。

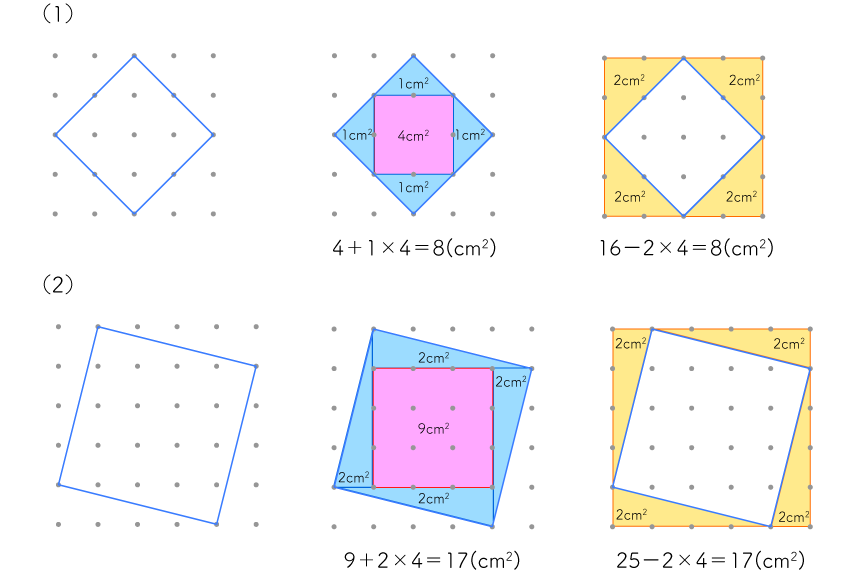
そして、(1)と(2)に共通する面積の求め方には、たとえば次の２つがあります。
・真ん中のピンクの正方形と、周りの水色の三角形４つを足す。
・全体の正方形から、周りの黄色の三角形４つを引く。
よって、(1)は8㎠、(2)は17㎠です。

正答率は、(1)が37.3％、(2)が19.1％でした。
(1)は、ひし形の面積の公式を使っても解けますので、５年生で学習したばかりのその知識を使ったことで、(2)よりも高めの正答率が出たのかもしれません。
しかし、どちらにしても、上記で示した面積を求める考え方を発想できない子が多かったことはわかります。

では、解答類型と反応率を見てみましょう。

(1)　４㎠：31.2％　９㎠：13.3％　６㎠：4.0％　16㎠：2.6％　３㎠：2.2％
　　12㎠：1.4％　10㎠：1.1％　２㎠：1.0％　12.5㎠：1.0％
　　無回答：1.2％　その他：3.7％

(2)　16㎠：34.0％　25㎠：14.1％　８㎠：4.6％　10㎠：2.6％　５㎠：2.2％
　　20㎠：1.9％　４㎠：1.8％　６㎠：1.4％　12㎠：1.1％　15㎠：1.1％
　　24㎠：1.1％　32㎠：1.1％　18㎠：1.0％　９㎠：0.8％
　　無回答：3.7％　その他：8.4％

(1)の誤答上位２つが４㎠と９㎠、(2)の誤答上位２つが16㎠と25㎠です。
つまり、どれも平方数（2×2=4、3×3=9、4×4=16、5×5=25）です。
このことから、「正方形の面積を求める」という問題から、１辺の長さを出して「１辺×１辺」で求めようと考えたのだと思われます。
子どもによく見られる、何となく見た感じから数値を適当に当てはめて答えを出すという典型的な行動です。

しかし、算数の学習内容では１辺の長さを出すことができません。
そこで、どうしたら答えが導き出せるかなと考えて欲しいところでしたが、そこまで考えられる児童は少なかったようです。

この問題のように、分割してから足してみたり、全体から引いてみたりという発想はとても大事で、見えない線が見えるようになる力を鍛えることにも繋がります。できなかった子は、ぜひしっかりと復習しておいて欲しいですね。