TOPICS

2024年度 第２回 ４級で正答率の低かった問題のご紹介です。
小学生でも考えられる問題ですが、いかに答えを導き出すかで思考力を必要とします。
すべて書き出して考えるという方法が最もシンプルですが、思考力を使って考える面白さもあります。ぜひ、小学生にも考えてもらいたいです。

【問題】
自然数を１から順に、４と９が含まれる数を除いて書いていきます。

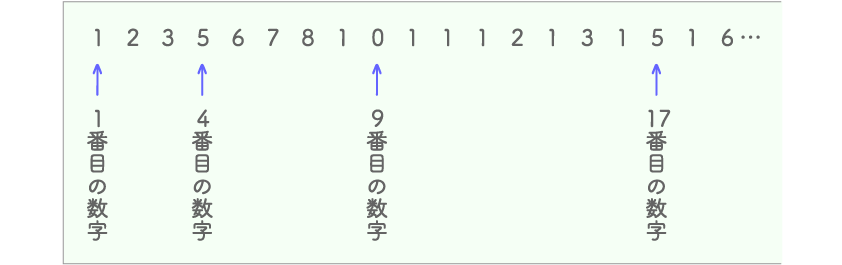
上の図のように、「１」「２」「３」の次は４を除くので「５」を書き、この「５」が４番目の数字になります。
「８」の次は９を除くので10ですが、10は１と０の２個の数字が使われているので 「１」「０」と書き、この「０」が９番目の数字になります。14、19などは４、９が含まれているので、十の位の１も書きません。
このように書いていくと、たとえば「１」から数えて17番目の数字は「５」になります。
60番目の数字を求めなさい。

まずは、文章からルールを理解することが重要ですが、このルールを正しく汲み取れていないような誤答も見受けられました。
では、考え方を見てみましょう。

【考え方】
１桁の自然数と２桁の自然数に分け、２桁の自然数は十の位の数ごとに、それぞれ何個の数字が使われているかを数えます。
まず、１から19まで数えると、次のようになります。

ここで、20～29、30～39も10～19と同じルールになるので、16個ずつになります。また、40～49にはすべて４が含まれているので、０個となります。
よって、１～49までの数は、7＋16＋16＋16＋0＝55（個）となり、50以降は次のようになるので、60番目は「５」となります。

すべて書き出していって数え上げるのも一つの方法ですが、ここでは10以降の２桁に規則性を見つけ出せるかどうかがポイントでした。

正答率は39.7％で、解答類型とその反応率は次のようになりました。

４：27.6％　１：3.4％　３：3.4％　６：1.7％　８：1.7％　９：1.7％
その他：15.6％　無解答：5.2％

「４」という解答が約30％もありましたが、これは次の図のように、40〜49についても同様に数えてしまった結果だと思います。

十の位を考慮することを忘れる間違いは、カレンダーの問題などでもよく見かけますので、典型的な間違いと言えるでしょう。

昨今、長めの文章からルールを読み取って考える問題が多く出題されます。
先にも書いたように小学生でも考えられる問題ですし、答える場所（80番目など）を変えたり、「５を除く」「８を除く」などルールを変えたりすれば、いろいろとアレンジができる問題です。

ぜひ、ルールを読み取って考える練習をしてみてください。