TOPICS

2024年度 第3回 算数・数学思考力検定の申し込み受付が1月6日から始まりました。

そこで、第2回で正答率の低かった問題の紹介とその分析をすることで、第3回の検定に向けてさらに思考力を育んでもらえたらと思います。

まず1回目は、10級の問題をご紹介します。

【問題】
算数と国語のテストが４回ずつありました。
ひとしさんの算数のテストの点数は、次のようになりました。
――――――――――――――――――――――
　・２回目は、１回目より３点下がりました。
　・３回目は、２回目より８点上がりました。
　・４回目は、３回目より６点下がりました。
――――――――――――――――――――――
算数のテストが高かった順に、回数を答えなさい。

【考え方】
ひとしさんの算数のテストの点数を線であらわすと、次のようになります。

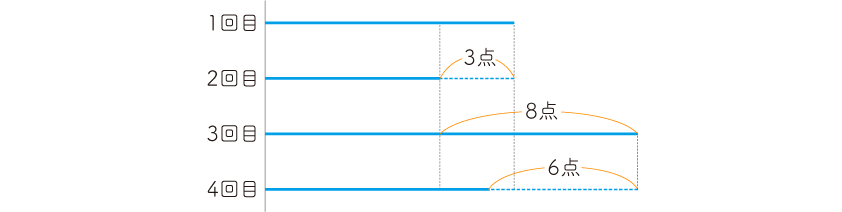
よって、点数が高かった順に、３回目→１回目→４回目→２回目　となります。


正解者は32.7％でした。

では、その他の解答類型とその反応率を見てみましょう。

３回目→１回目→２回目→４回目：18.1％
３回目→４回目→１回目→２回目：10.8％
３回目→２回目→４回目→１回目：5.3％
３回目→２回目→１回目→４回目：4.8％
３回目→４回目→２回目→１回目：4.0％
その他：24.3％

ちなみに、その他24.3％のうち、いちばん点数が高かった回を３回目と答えた児童は4.8％いました。
つまり、正解者も含めて、いちばん点数が高かった回は３回目だということがわかった児童は80.2％となります。

これは、３回目のみ「上がった」という表現を使っていることから、わかりやすかったのかもしれません。

しかし、具体的に点数が問題文に示されていない中で考えることが、10級を受けた児童にとっては難しかったのでしょう。

このような問題は、具体的に数値を入れて考えてみるのもよいですね。
例えば、１回目を50点としてみましょう。
すると、次のように、２回目が47点、３回目が55点、４回目が49点となり、具体的な数値で比較できるので、考えやすくなります。

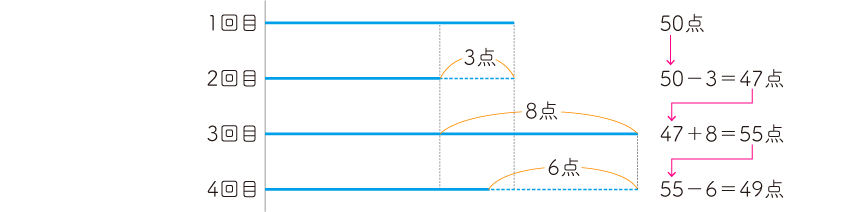
この問題は、具体的な数値が示されていないのときに、相対的に比較して考える問題ですが、数値を適当において考えてみようと思いつく過程でも思考力が伸びます。

間違えてしまった子には、次の◯の部分を変えて、何度も考えさせてみるとよいでしょう。
――――――――――――――――――――――
　・２回目は、１回目より◯点◯がりました。
　・３回目は、２回目より◯点◯がりました。
　・４回目は、３回目より◯点◯がりました。
――――――――――――――――――――――