TOPICS

第１回 で正答率の低かった問題の紹介６回目。今日は５級の問題です。
前回の６級の問題に続き、今回も数を規則的に山の形に並べていく問題です。
わかりやすい規則性なのですが、いかにミスなく計算するかというところで間違えた人が多かったのだと思われます。
では、見ていきましょう。

【問題】
次の数の列は、自然数をある規則にしたがって並べたものです。14段目に並ぶすべての数の和を求めなさい。

【考え方】
まず、左端の数を見てみると、１段目から順に、1、3、5、7、…と２ずつ増えています。つまり、ｎ段目の左端の数は 2n − 1 と表すことができます。
また、各段に並んでいる数の個数は、１段目から順に、１個、２個、３個、４個、…です。つまり、ｎ段目に並んでいる数の個数はｎ個です。

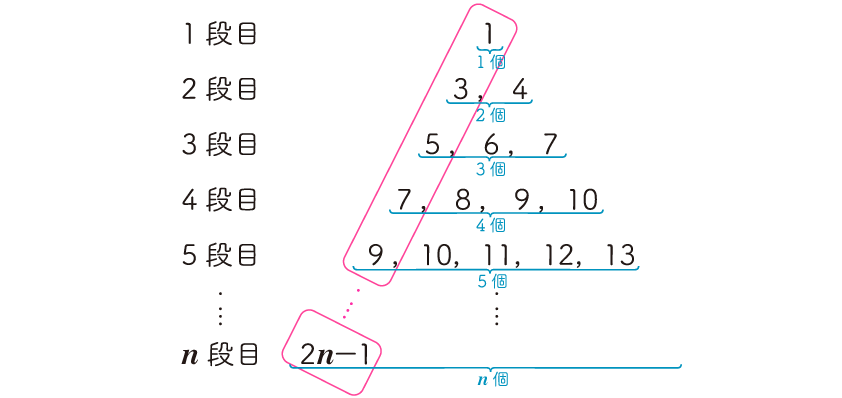
つまり、14段目の左端の数は 2 × 14 − 1 ＝ 27 で、14段目には、27、28、29、30、31、32、33、34、35、36、37、38、39、40と14個の数が並びます。

なお、左端の数の一般式が 2n − 1 ということがわからなくても、1、3、5、7、9、11、13、15、17、19、21、23、25、27と順に書き出していけばわかります。

ですので、14個の数の並びを求めるまでは、それほど難しくありません。

問題は、27 ＋ 28 ＋ 29 ＋ 30 ＋ 31 ＋ 32 ＋ 33 ＋ 34 ＋ 35 ＋ 36 ＋ 37 ＋ 38 ＋ 39 ＋ 40の計算です。
答えは469なのですが、この計算を間違えた人が一定数いました。

では、どのように考えるとミスなく計算できるか。
そこを考えてみましょう。

次のように、27 ＋ 28 ＋  …の式を左右反対にしたものを上下に並べ、その上下の数を足します。すると、67を14個足した式になりました。

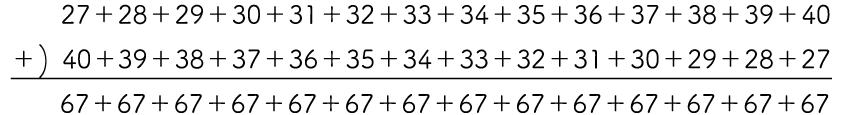
この式は、求める数の２倍になっているので、
その合計は 67 × 14 ÷ 2 ＝ 67 × 7 ＝ 469 となります。

この計算方法は「ガウスの計算」として有名ですね。

規則性がある数の列の合計を求めるときはこの計算方法が使えることがよくあるので、この計算方法を知っておくとよいですね。