TOPICS
思考力検定
2024年07月14日
正答率の低かった問題の紹介(2023年度 第3回 4級)
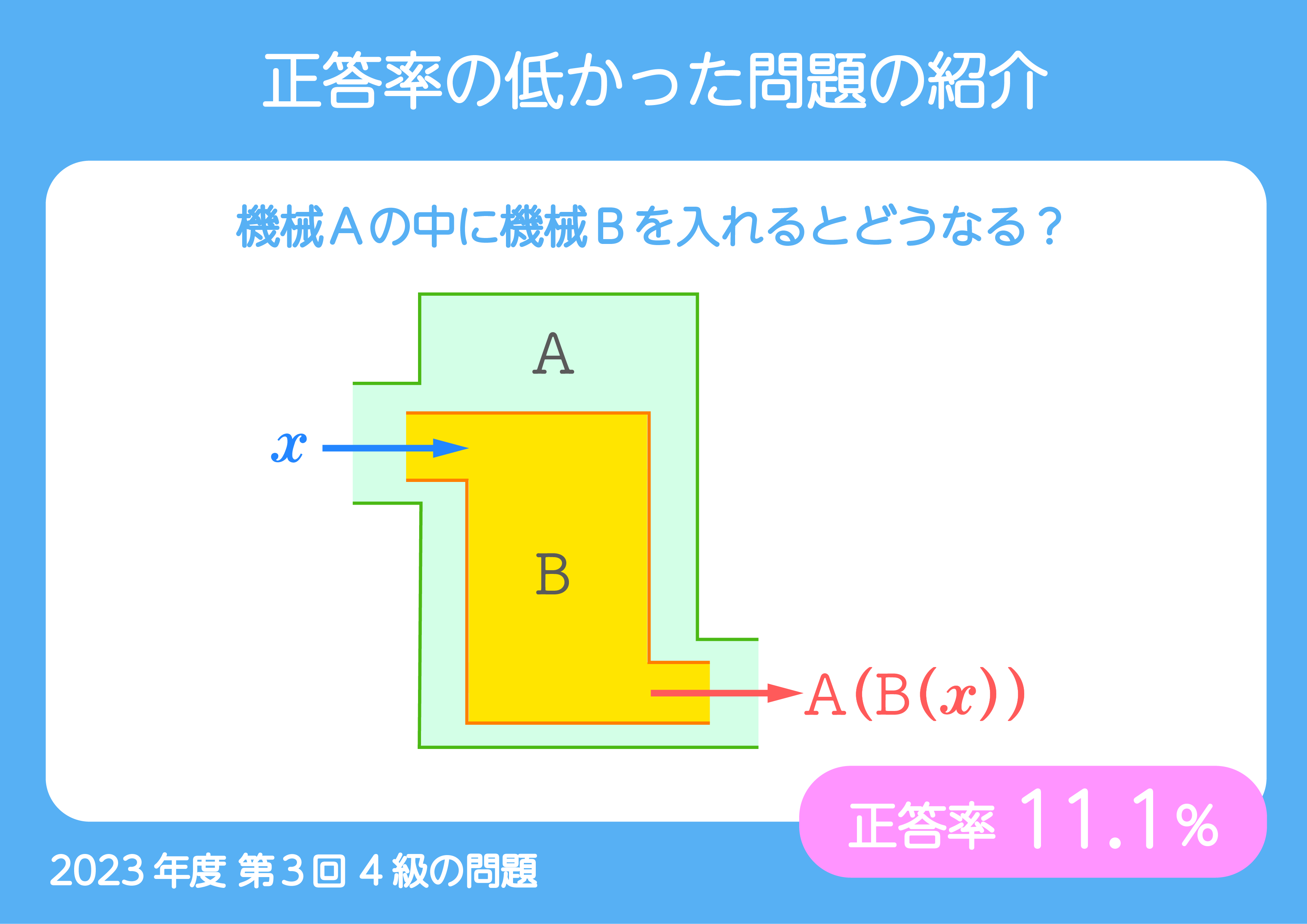
今回は、2023年度第3回4級の問題です。
算数ラボ8級に、「ある数を機械に入れると、違う数が出てくる」問題がありますが、今回4級で出題したのは、その機械を入れ子にするとどうなるかを考える問題です。
では、問題を見てみましょう。
【問題】
数を入力すると、次の計算をして数を出力する3つの装置があります。
装置A:入力した数から3をひいた数を出力する。
装置B:入力した数を2分の1倍してから4をひいた数を出力する。
装置C:入力した数を- 2倍してから1をたした数を出力する。
装置A、B、Cにある数 x を入力したとき、出力される数をそれぞれ A(x)、B(x)、C(x) と表すことにします。
A(B(x)) = B(C(x)) のとき、xの値を求めなさい。
【考え方】
装置A、B、Cを算数ラボ8級のように図で表すと、次のようになります。
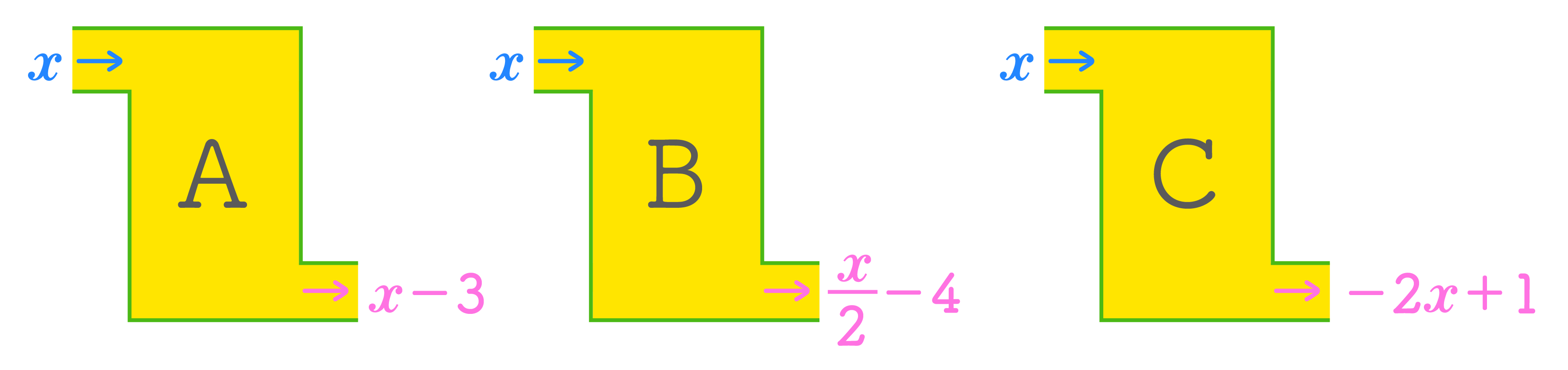
たとえばxに6を入れると、次のようになります。
A(x)=6−3=3
B(x)=6/2−4=−1
C(x)=−2×6 +1=−11
では、A(B(x)) や B(C(x)) の意味を考えましょう。
A(B(x))は、AにB(x)を入力することを表し、B(x)はBにxを入力することを表しています。
つまり、xをBに入力し、出てきたB(x)をAに入力することを意味します。
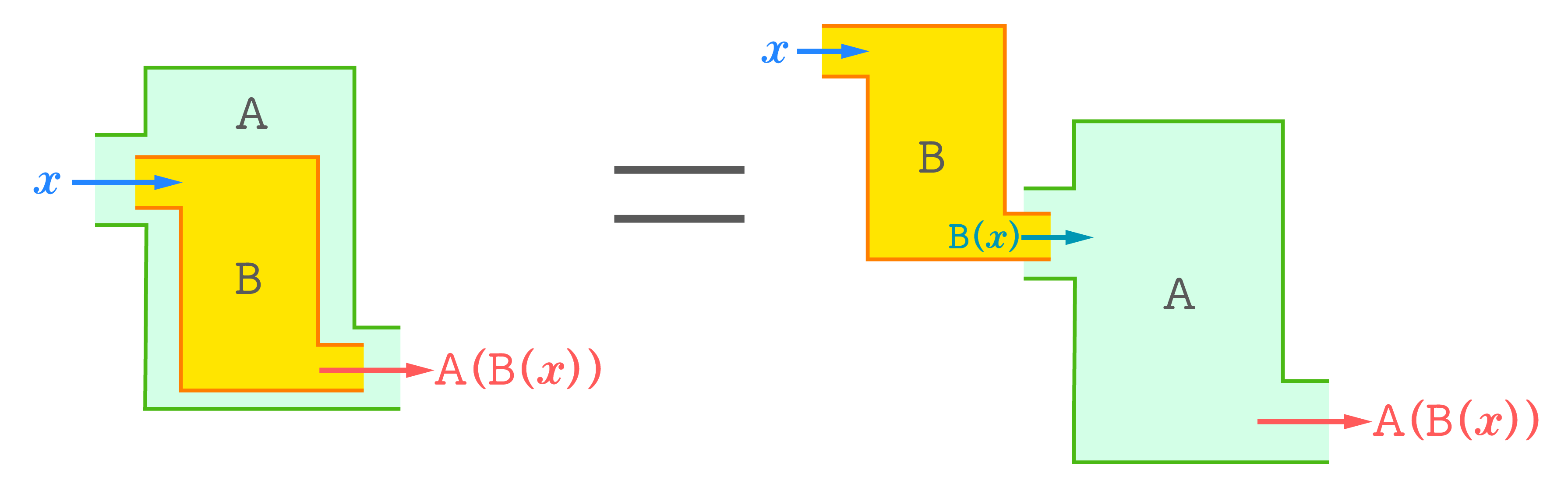
つまり、A(x)=x−3、B(x)=x/2−4 なので、
A(B(x))= (x/2 −4)−3=x/2 −7 となります。
同様に、B(x)=x/2−4、C(x)=−2x+1 なので、
B(C(x))=(−2x+1)/2−4=−x−7/2 となります。
この2つの式が等しいので、x/2−7=−x−7/2 をxについて解くと、
x=7/3 となります。
この問題は、無回答者が37.8%もおり、難しかったものと思われます。
また、正解者と無回答者を除いた残りの約50%においても、特徴的に偏った解答類型は見られませんでした。
なお今回は、飛び級で小学生が受けた割合も多かったので、問題の意図を理解するのが難しかったのかもしれません。そのような影響で、解答類型とその反応率においても、特徴的な間違いというものが現れなかったのかと思われます。
また、期間を空けて、類題を出題して確認してみたいと思います。
